- ...
「それが専門です」ということにしているけれど1
- 脱線かもしれないが、
大学院で指導するときは
「研究テーマはなるべく偏微分方程式の数値計算法にして下さい」
ということにしているが、学部卒研では研究テーマは自由としている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
常微分方程式2
- 微分方程式は、
独立変数の個数が1であるとき常微分方程式 (ordinary differential equation)、
2以上であるとき偏微分方程式 (partial differential equation) と呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
学部ゼミの卒業研究でも現象のモデルとして良く現れる3
- 常微分方程式自体がある現象のモデルとなることも多いし、
偏微分方程式を扱うために常微分方程式が必要になることも多い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... CLASS="textbf">時定数4
- 時定数は「ときていすう」とも読むそうだ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... と呼ぶ5
- しばしば「積分する」という言葉は、
微分方程式を解く、という意味に使われる。多分「解」
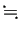 「積分」というニュアンスだろう (と個人的に考えている)。
「積分」というニュアンスだろう (と個人的に考えている)。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
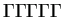 6
6
- いわゆる硬い方程式など、
古典的Runge-Kutta法では手に余る問題もあり、それはそれで重要であるが。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... と呼んで区別することがある7
- 私は学生のとき、
厳密解に対して「真の解」という表現を使ったことがあるが、
「言わんとすることは分かるけれど、それは普通に使われる表現ではない。
厳密解と言いなさい。」と指導された記憶がある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
比較的簡単で、高精度な解が得られるため、良く用いられる方法として8
- 長い間定番の方法であったが、
最近は常微分方程式を解く部分は自分でプログラムを書かないようになりつつあり、
古典的 Runge-Kutta 法が採用されるのは、そろそろ変わる
(つまりもっと凝ったアルゴリズムが使われることが増えてくる)
のかもしれない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ということ)9
- Euler法も
Runge-Kutta法も Runge-Kutta 型公式と呼ばれる分類に属する
(詳しくは専門書を見て下さい)。
Runge-Kutta 型公式は、
計算の途中で時間刻み
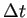 を変更することが簡単という
という長所があり、実際に刻み幅の自動調節がしばしば行われる。
を変更することが簡単という
という長所があり、実際に刻み幅の自動調節がしばしば行われる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(equilibrium10
- [ì:kwlíbrim]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... とよぶ11
- 数学以外の分野では、「位相空間」とよぶこともあるが、
数学では「位相空間」は topological space の訳語として使われるので、
phase space を「相空間」とよぶのが普通である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...被食者の関係にある2種の生物種について
12
- 英語では、捕食者は predator, 被食者は prey という。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (自力で解くのは難しいかも13
- この課題が解けたら、1つでS評価級。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... だけで定まるのは不思議14
- 周期解であるから、
1つの解軌道のどこから出発しても同じになるのは明らかであるが、
解軌道が違っても、たとえば平衡点のごく近くをまわっても、
平衡点から遠く離れたところをまわっても、
平均値がまったく変わらないというのは、それほど明らかではない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
個体数に比例して採ることになると考えて15
- 本来食用魚が欲しいのに軟骨魚も採ってしまうのは、
網を使った漁をしているからだろうか。
同じ割合
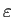 を用いているのが気になるが、
を用いているのが気になるが、
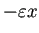 ,
, 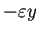 をそれぞれ
をそれぞれ
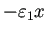 ,
, 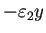 で置き換えると、
で置き換えると、
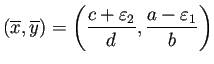 となるだけで、
食用魚が減って軟骨魚類が増えるという結論は変わらない。
となるだけで、
食用魚が減って軟骨魚類が増えるという結論は変わらない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... より小さいと感染者数は減少して16
- このことを
「流行は起こらない」といい、一時的にでも感染者数が増加することを
「流行が起こる」というようである。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... も無次元量であり、単位を持たない17
- 例えば、
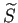 ,
,
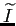 ,
,
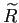 はどれも、
人数を人数で割ったものなので単位なし(次元も無次元)である。
はどれも、
人数を人数で割ったものなので単位なし(次元も無次元)である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... の処理系は普通はインタープリターなので18
- 多くのプログラミング言語処理系は、
コンパイラーとインタープリターに分類される。
その言語で書かれたプログラムを実行可能な機械語プログラムに翻訳することを
コンパイルといい、翻訳するソフトウェアのことをコンパイラーと呼ぶ。
また、その言語で書かれたプログラムを解釈して実行するソフトウェアを
インタープリター (普通は通訳という意味) と呼ぶ。
C 言語や C++ 言語の処理系は、コンパイラーであるのが普通である。
一方、Python 処理系はインタープリターである。
Java は、Java 言語で書かれたプログラムを中間言語にコンパイルした上で、
中間言語を実行できるプログラム (JVM -- Java Virtual Machine)
で実行するので、コンパイラーとインタープリターの中間であると言える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
十分な計算速度が得られるか心配になるが19
- その理由から、
私は Julia や Crystal に注目している。
これらはJIT (just in time) compilter を用いることで実行効率を高めている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ndarray20
- ndarray は Python の Numpy で定義された用語である。
https://docs.scipy.org/doc/numpy-1.13.0/reference/arrays.ndarray.html
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... も任意定数である21
- これは
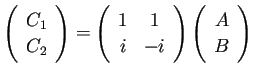 において係数行列が正則であることから分かる。実際、
において係数行列が正則であることから分かる。実際、
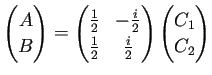 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
一方で解が存在すること自体を保証する方法22
- 例えば、
高校数学の段階でも、方程式の解を具体的に式で表示できなくても、
グラフによる考察
(曲線と曲線が交わる -- 厳密には中間値の定理を根拠とする)
から解の存在の証明せよ、あるいは解の個数を調べよ、
という問題があった。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
有名である23
- Rudolf Otto Sigismund Lipschitz
(1832-1903, Königsberg に生まれ、Bonn にて没する) にちなむ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... の領域または閉領域とする24
- 領域とは連結開集合のこと。また閉領域とは、
ある領域の閉包になっている集合のこと (
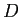 が閉領域とは、
ある領域
が閉領域とは、
ある領域 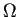 が存在して、
が存在して、
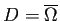 が成り立つこと) 。
が成り立つこと) 。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
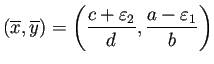 となるだけで、
食用魚が減って軟骨魚類が増えるという結論は変わらない。
となるだけで、
食用魚が減って軟骨魚類が増えるという結論は変わらない。
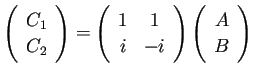 において係数行列が正則であることから分かる。実際、
において係数行列が正則であることから分かる。実際、
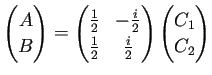 .
.