Next: 5.7 解の周期性 Up: 5 Lotka-Volterraの方程式 (捕食者被食者の数理モデル) Previous: 5.5 平衡点とその安定性
まず、実は少し問題含みであるけれど、多くのテキストに載っていて、 見通しのよい議論を紹介する。
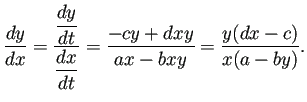
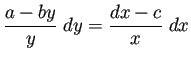
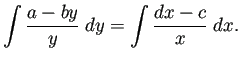
以上の議論は分かりやすいが、いくつか問題がある。
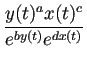 が定数であることが、
が定数であることが、
まず分母0の問題を片付けよう。次の定理が成り立つ。
|
|
発見的考察、というのをやろう。
![]() を (形式的に) (C.17) に代入すると
を (形式的に) (C.17) に代入すると
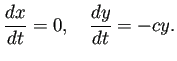
同様に ![]() から
から ![]() ,
,
![]() という解を発見できる
(「捕食者がいなければ被食者は限りなく増え続ける」ということである)。
「
という解を発見できる
(「捕食者がいなければ被食者は限りなく増え続ける」ということである)。
「![]() 軸の正の部分は解軌道である」ということが分かった。
軸の正の部分は解軌道である」ということが分かった。
最後に、原点は平衡点であるから、原点1点からなる集合は解軌道である。
以下、![]() ,
, ![]() である解だけを考えることにすると、
である解だけを考えることにすると、
![]() ,
, ![]() . ゆえに
. ゆえに ![]() ,
, ![]() である。
微分方程式から
である。
微分方程式から
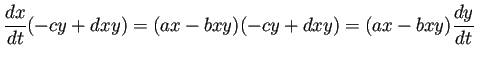 |
(5.6) |
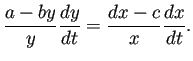 |
(5.7) |
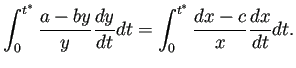
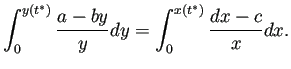
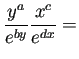 定数 定数 |
(5.8) |
関数
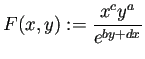 は、第1象限ではつねに正の値を取り
は、第1象限ではつねに正の値を取り
![]() のとき最大値を取る。
のとき最大値を取る。
![]() を
を ![]() 軸や
軸や ![]() 軸上の点に近づけると、
軸上の点に近づけると、
![]() .
.
![]() を満たす任意の
を満たす任意の ![]() に対して、
に対して、
(もちろん図を描けば「明らか」である。証明できた人はレポートしよう。)
(5.9)
が解軌道を表す方程式である。
後で、
![]() は周期関数で、
方程式の定める閉曲線の周りをぐるぐる回る
(ゆえに解軌道は閉曲線に一致する)
ことが分かるが、
現時点では解が存在する任意の時刻
は周期関数で、
方程式の定める閉曲線の周りをぐるぐる回る
(ゆえに解軌道は閉曲線に一致する)
ことが分かるが、
現時点では解が存在する任意の時刻 ![]() で、
で、
![]() がその曲線の上にあることだけが分かっている。
がその曲線の上にあることだけが分かっている。
(ヒント: 色々なやり方があると思われるが、一つの方針を示す。
背理法を用いる。
解がある有限の ![]() に対して、
に対して、
![]() まで存在するが、
まで存在するが、![]() を超えては延ばせないと仮定する。
得られた解軌道の方程式から、任意の解軌道は有界であることが分かる。
それから、任意の解軌道の上で
を超えては延ばせないと仮定する。
得られた解軌道の方程式から、任意の解軌道は有界であることが分かる。
それから、任意の解軌道の上で ![]() が有界であると分かる。
それから極限
が有界であると分かる。
それから極限
![]() が存在することが導かれる。
そうすると解は
が存在することが導かれる。
そうすると解は ![]() まで延長され、
さらに
まで延長され、
さらに ![]() を超えて延長できることが導かれる。
これは背理法の仮定に矛盾する。ゆえに
を超えて延長できることが導かれる。
これは背理法の仮定に矛盾する。ゆえに
![]() で解が存在する。
-- 桂田 [22] §8.3 に少し書いておいた。)
で解が存在する。
-- 桂田 [22] §8.3 に少し書いておいた。)
桂田 祐史