5.7 解の周期性

$(c/d,a/b)$ 以外の第1象限内の点では

$$\left(\frac{\D x}{\D t},\frac{\D y}{\D t}\right)\ne(0,0),\quad \left\vert\left(\frac{\D x}{\D t},\frac{\D y}{\D t}\right)\right\vert>0.$$

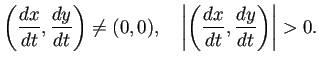
$(c/d,a/b)$ を通らない任意の解軌道で、速さはある正定数以上である。

証明: 第1象限内の、平衡点 $(c/d,a/b)$ 以外の解 $(x(t),y(t))$ に対して、

$$L:=F(x(0),y(0))$$

で $L$ を定めると、 $(x(t),y(t))$ はつねに閉曲線 $F(x,y)=L$ 上にあり、 閉曲線は $\mathbb{R}^2$の有界閉集合であるから、 連続関数である速さは閉曲線上で最小値 (当然正の値)を持つ。 $\qedsymbol$

すなわち、ある一定値以上の速さで運動する。 曲線の長さは有限だから、いつかは $(x(0),y(0))$ に戻って来る。 このことから、 $(x(t),y(t))$ は周期関数であることが証明できる。

課題 5.7.1   $T>0$, $(x(T),y(T))=(x(0),y(0))$ ならば、 $(x(t),y(t))$ は周期 $T$ の周期関数であることを示せ。

以上の論法は、応用が効く。

課題 5.7.2   単振り子では、鉛直線から測った角度 $\theta(t)$ が

$$\frac{\D^2\theta}{\D t^2}=-\frac{g}{\ell}\sin\theta$$

という微分方程式に従う ($g$ は重力加速度、$\ell$ は振り子の糸の長さ、 ともに正の定数)。 この微分方程式の(ほとんどすべての)解が周期関数であることを示せ。

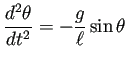
(コメント: 楕円関数を用いると、単振り子の運動の厳密解を表すことが出来るが、 楕円関数を知らなくても、 Lotka-Volterra 方程式と同じ論法で周期解の存在が示せる。)