Next: 5.9 1つのルーツの紹介: D'Ancona の疑問と Up: 5 Lotka-Volterraの方程式 (捕食者被食者の数理モデル) Previous: 5.7 解の周期性
平衡点 ![]() 以外の第1象限内の任意の解
以外の第1象限内の任意の解
![]() は、
周期関数であることを示した。その周期を
は、
周期関数であることを示した。その周期を ![]() として
として
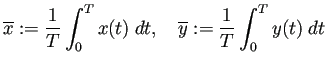 |
(5.10) |
(F.4) を証明しよう。
まず微分方程式から
![$\displaystyle \int_0^T\frac{x'(t)}{x(t)}\Dt
=\left[\log x(t)\right]_0^T
=\log x(T)-\log x(0)=0.
$](img311.png)
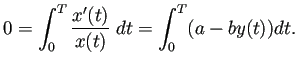
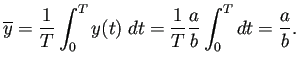
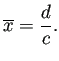
![]() の平均
の平均
![]() が平衡点であることは、
なるほどと感じる人が多いであろう
(平衡点を通る解の平均値が平衡点そのものであることは明らかであるが、
そうでない場合にもそうなっている、ということである)。
が平衡点であることは、
なるほどと感じる人が多いであろう
(平衡点を通る解の平均値が平衡点そのものであることは明らかであるが、
そうでない場合にもそうなっている、ということである)。