G..1 力学系とは

この文書では、微分方程式として

$$\frac{\D x}{\D t}(t)=f(x(t),t)$$

という形のもの (1階正規形微分方程式) を考えた。特別な場合として、 関数 $f(x,t)$ が $t$ に依らない場合がある。 その場合は単に $f(x)$ と書けば良いので、微分方程式は

$$\frac{\D x}{\D t}(t)=f(x(t)) \dfrac{\D x}{\D t}=f(x)$$ (G.1)

という形になる。

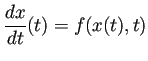
これを自励系微分方程式 (autonomous differential equation, autonomous system, 自律系とも訳される) という。 力学系 (dynamical system) と呼ばれることも多い。

一つ注意が必要である。 力学系という言葉は、微分方程式でない場合にも使われる (広い意味を持っている、ということである)。 ネットで検索したりすると混乱するかもしれない。

上で「特別な場合」と書いたが、 応用上出て来る微分方程式で力学系であるものは非常に多い。 つまり「完全に一般ではなく、特別ではあるが、 応用上は十分一般性が高い」。 実際、この文書に現れる微分方程式で力学系でないものは、 強制振動の方程式 (C.22) くらいである。 従って、力学系に焦点を当てた議論は学ぶ価値がある。