Next: C..2.5.1 証明 (線形空間の議論に慣れている人向け) Up: C..2 基本的な定理の証明 Previous: C..2.4.2 [, の次独立性]
微分方程式
実は指数関数 ![]() は、複素変数に一般化され、
その一般化された指数関数に対しても
は、複素変数に一般化され、
その一般化された指数関数に対しても
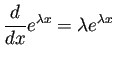
| 要約: 複素変数の指数関数 |
|
指数関数は複素変数まで拡張できる。
その定義には色々な方法があるが、どれを採用しても結果は一致する。
ここでは
|
![]() ,
, ![]() が実定数の場合、
が実定数の場合、
![]() が虚根を持てば、
それは互いに複素共役である。ゆえに
が虚根を持てば、
それは互いに複素共役である。ゆえに
![]() ,
,
![]() とおくと、
とおくと、
補足
特性根が虚数である場合を定理の形にまとめておかなかったが、
そうしておくべきであった。

|
この文書では (元々の対象者が大学1年生であることから)、 証明はなるべく初等的にする方針で説明しているが、 ここではまず線形空間の議論に慣れている人向けの証明をして、 それから初等的な(だがやや面倒な)証明を示すことにする。
![]() 階線形同次微分方程式に対し、
階線形同次微分方程式に対し、