5.9 1つのルーツの紹介: D'Ancona の疑問と Volterraの回答

Volterra が、このモデルを考えたのは、 そもそも D'Anconaダンコナ から質問(相談)されたことがきっかけであった。

D'Ancona の疑問

第1次世界大戦中 (1914-1918)に、 漁業は小規模にしか行えなかったにもかかわらず、 食用に適さない軟骨魚類 (サメやエイなど) が大戦前よりも増え、 食用魚は減ってしまったのはなぜか (漁をあまりしなかったのだから増えているのでは？)

という D'Ancona の問に対して、 Volterra は微分方程式のモデルを作って、 その解析に基づいた解答を与えた。 これが Lotka-Volterra方程式の1つの由来である。

これは有名な話で、色々なテキストで紹介されているが、 ブラウン [42] の説明が詳しくて分かりやすく、私のお勧めである。

(数学以外の事実の説明をある程度詳しく書かないと、分かりにくいし、 面白くないのではと思われるが、以下に数学的な部分だけ抜書きしておく。 [42] の出来の悪い引き写しにしかならない可能性が高いが…)

人間が漁業をすることにより、食用魚と軟骨魚を採っている効果を考える。 個体数に比例して採ることになると考えて ¹⁵、

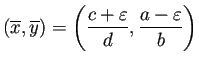
に従うと仮定しよう (ここで$\eps$は正の定数)。 これは (5.1a), (5.1b) で、 $a$ を $a-\eps$, $c$ を $c+\eps$ に置き換えたものである。 ゆえに §G.3 の議論から、 $(x(t),y(t))$ の平均 $\left(\overline{x},\overline{y}\right)$ は

$$(\overline{x},\overline{y})=\left(\frac{c+\eps}{d},\frac{a-\eps}{b}\right)$$

である。まとめると

• 平時 (漁業操業している場合) の平均 $\left(\frac{c+\eps}{d},\frac{a-\eps}{b}\right)$
• 戦争中 (あまり漁業操業していない場合) の平均 $\left(\frac{c}{d},\frac{a}{b}\right)$

したがって、戦争中は平時と比べて、食用魚が( $\frac{c+\eps}{d}$ → $\frac{c}{d}$)減り、軟骨魚類が ( $\frac{a-\eps}{b}$ → $\frac{a}{b}$) 増える。 ゆえに戦争中は魚類全体に占める軟骨魚類の率が上がるはずである。

表 1: イタリアのフューメ港での 1914-1923年の軟骨魚類の漁獲量率のデータ ([42] から引用)

1914	1915	1916	1917	1918	1919	1920	1921	1922	1923
11.9%	21.4%	22.1%	21.2%	36.4%	27.3%	16.0%	15.9%	14.8%	10.7%