5.2 Lotka-Volterra方程式

複数の生物種の相互作用には、色々な場合があるが、 捕食者-被食者の関係にある2種の生物種について ¹²、 Lotka と Volterra は独立に次の方程式によるモデルを提案した。

(注: 捕食者-被食者モデル (Predator-prey model) には、 他にも色々ある。)

$x(t)$, $y(t)$は、それぞれ時刻$t$における被食者の個体数、 捕食者の個体数を表す。 $a$, $b$, $c$, $d$ は正の定数である。

(5.1a), (5.1b) を Lotka-Volterra の方程式 (Lotka-Volterra equations) とよぶ。

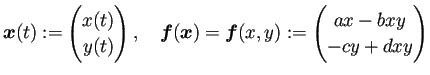$$\bm{x}(t):=\begin{pmatrix}x(t)\\ y(t) \end{pmatrix}, \quad \bm{f}(\bm{x})=\bm{f}(x,y):=\begin{pmatrix}ax-bxy \\ -cy+dxy\end{pmatrix}$$ (5.2)

とおくと、 (5.1a), (5.1b) は次のように表される。

$$\frac{\D\bm{x}}{\D t}(t)=\bm{f}(\bm{x}(t)).$$ (5.3)