Next: 7 ŠîĹŠłŽŔ¬▓Úíî Up: 6 SIRŃâóŃâçŃâź Previous: 6.3 ŠĽ░ňşŽšÜäŔžúŠ×É (1)
ŠťëňÉŹŃü¬ňč║ŠťČň揚öčšöúŠĽ░ (basic reproduction number) ŃüĘŃüŁŃü«ŠäĆňĹ│
(ŃÇîňč║ŠťČň揚öčšöúŠĽ░Ńüî ![]() ŃéłŃéŐň░ĆŃüĽŃüäŃüĘŠäčŠčôŔÇůŠĽ░Ńü»ŠŞŤň░ĹŃüŚŃüŽ16ŃÇü
ŃéłŃéŐň░ĆŃüĽŃüäŃüĘŠäčŠčôŔÇůŠĽ░Ńü»ŠŞŤň░ĹŃüŚŃüŽ16ŃÇü
![]() ŃéłŃéŐňĄžŃüŹŃüäŃüĘŃüŚŃü░ŃéëŃüĆŃü«ÚľôŃü»ňóŚŃüłŃéő (ŠÁüŔíîŃüÖŃéő)ŃÇŹÔÇŽ
-- ŃüôŃéîŃéĺŃüäŃüŹŃüíŃüĺŃéôŃéŐÚľżňÇĄňÄčšÉćŃüĘňĹ╝ŃüÂŃüôŃüĘŃüîŃüéŃéő)
ŃéĺŔ¬ČŠśÄŃüÖŃéőŃÇé
ŃéłŃéŐňĄžŃüŹŃüäŃüĘŃüŚŃü░ŃéëŃüĆŃü«ÚľôŃü»ňóŚŃüłŃéő (ŠÁüŔíîŃüÖŃéő)ŃÇŹÔÇŽ
-- ŃüôŃéîŃéĺŃüäŃüŹŃüíŃüĺŃéôŃéŐÚľżňÇĄňÄčšÉćŃüĘňĹ╝ŃüÂŃüôŃüĘŃüîŃüéŃéő)
ŃéĺŔ¬ČŠśÄŃüÖŃéőŃÇé
Šľ╣šĘőň╝ĆŃéĺŃüäŃéĆŃéćŃéőšäíŠČíňůâňîľŃüŚŃüŽŃÇüš░튯öŃü¬ňŻóŃüźňĄëŠĆŤŃüŚŃüŽŃüőŃéëŔ¬ČŠśÄŃüÖŃéőŃÇé
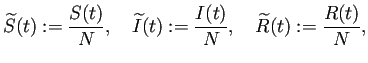
ŃüôŃü«ŃüĘŃüŹŠČíň╝ĆŃüÉŃéŐšźőŃüĄŃÇé
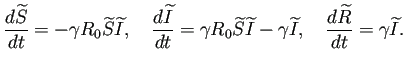 |
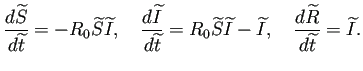 |
ń╗ąńŞŐŃéĺŃüżŃüĘŃéüŃüŽŃüŐŃüĆŃÇé
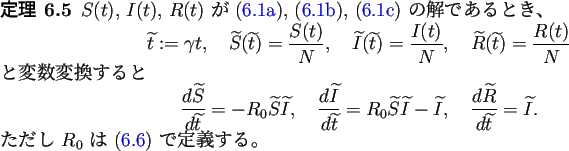
|
ŃééŃüĘŃééŃüĘ ![]() ,
, ![]() ,
, ![]() Ńü»ňÇőńŻôŠĽ░ (ń║║ňĆú) Ńü¬Ńü«ŃüžňŹśńŻŹŃü»ńżőŃüłŃü░ŃÇîń║║ŃÇŹŃÇü
Ńü»ňÇőńŻôŠĽ░ (ń║║ňĆú) Ńü¬Ńü«ŃüžňŹśńŻŹŃü»ńżőŃüłŃü░ŃÇîń║║ŃÇŹŃÇü
![]() Ńü»ŠÖéňł╗Ńü¬Ńü«ŃüžňŹśńŻŹŃü»ńżőŃüłŃü░ŃÇąŃÇŹŃüžŃüéŃéőŃüîŃÇü
Ńü»ŠÖéňł╗Ńü¬Ńü«ŃüžňŹśńŻŹŃü»ńżőŃüłŃü░ŃÇąŃÇŹŃüžŃüéŃéőŃüîŃÇü
![]() ,
,
![]() ,
,
![]() ,
,
![]() , ŃüŁŃüŚŃüŽ
, ŃüŁŃüŚŃüŽ ![]() ŃééšäíŠČíňůâÚçĆŃüžŃüéŃéŐŃÇüňŹśńŻŹŃéĺŠîüŃüčŃü¬Ńüä
17ŃÇé
ŃééšäíŠČíňůâÚçĆŃüžŃüéŃéŐŃÇüňŹśńŻŹŃéĺŠîüŃüčŃü¬Ńüä
17ŃÇé
![]() ,
,
![]() ,
,
![]() Ńü»ŃÇü
ŃüŁŃéîŃü×ŃéîŠäčňĆŚŠÇžŔÇůŃÇüŠäčŠčôŔÇůŃÇüÚÖĄňÄ╗ŔÇůŃü«ňůĘńŻô(ňůĘń║║ňĆú)ŃüźňŹáŃéüŃéőšÄçŃüžŃüéŃéőŃÇé
COVID-19Ńü«šČČ1Š│óŃüžŃü»ŃÇü
Ńü»ŃÇü
ŃüŁŃéîŃü×ŃéîŠäčňĆŚŠÇžŔÇůŃÇüŠäčŠčôŔÇůŃÇüÚÖĄňÄ╗ŔÇůŃü«ňůĘńŻô(ňůĘń║║ňĆú)ŃüźňŹáŃéüŃéőšÄçŃüžŃüéŃéőŃÇé
COVID-19Ńü«šČČ1Š│óŃüžŃü»ŃÇü
![]() ŃüžŃüéŃüúŃüčŃüĘŔĘÇŃéĆŃéîŃüŽŃüäŃéő
(ŃüŁŃüćń╗«ň«ÜŃüŚŃüŽŃéĚŃâčŃâąŃâČŃâ╝ŃéĚŃâžŃâ│ŃüîŔíîŃéĆŃéîŃüč)ŃÇé
ŃüôŃü«ňá┤ňÉłŃÇü
ŃüžŃüéŃüúŃüčŃüĘŔĘÇŃéĆŃéîŃüŽŃüäŃéő
(ŃüŁŃüćń╗«ň«ÜŃüŚŃüŽŃéĚŃâčŃâąŃâČŃâ╝ŃéĚŃâžŃâ│ŃüîŔíîŃéĆŃéîŃüč)ŃÇé
ŃüôŃü«ňá┤ňÉłŃÇü
![]() Ńü»
Ńü» ![]() ŠŚąŃéĺňŹśńŻŹŃüĘŃüŚŃüŽŠŞČŃüúŃüčŠÖéňł╗ŃüĘŃüäŃüćŃüôŃüĘŃüźŃü¬ŃéőŃÇé
ŠŚąŃéĺňŹśńŻŹŃüĘŃüŚŃüŽŠŞČŃüúŃüčŠÖéňł╗ŃüĘŃüäŃüćŃüôŃüĘŃüźŃü¬ŃéőŃÇé
ń╗ąńŞőŃüžŃü»ŃÇü
![]() ŃéĺšťüŃüäŃüŽ
ŃéĺšťüŃüäŃüŽ
ňŹśńŻŹŃé劍┐ŃüłŃüčŃüáŃüĹŃü¬Ńü«ŃüžŃÇüňůâŃü«ňĽĆÚíîŃüĘŠťČŔ│¬šÜäŃü¬ÚüĽŃüäŃüîŃüéŃéőŔĘ│ŃüžŃü»Ńü¬ŃüäŃÇé ŠČíŃü«2ŃüĄŃü«ň«ÜšÉćŃü»ŃÇüń║îŃüĄšŤ«Ńü« (5), (6) ń╗ąňĄľŃü»ňëŹŃü«ň«ÜšÉćŃüžŔĘ╝ŠśÄŃüÜŃü┐ŃüĘŃüŚŃüŽŔë»ŃüäŃÇé
![\begin{jtheorem}
% latex2html id marker 1455
\begin{enumerate}[(1)]
\item
$S(t...
...ref{eq:šäíŠČíňůâšžĹSIR2}) Ńü«ŔžúŔ╗îÚüôŃüžŃüéŃéőŃÇé
\end{enumerate}\end{jtheorem}](img447.png)
|
![\begin{jtheorem}
$S(0)>0$, $I(0)>0$\ ŃüĘń╗«ň«ÜŃüÖŃéőŃÇé
\begin{enumerate}[(1)]
...
...ŁŠťčňÇĄŃüźň»żŃüŚŃüŽ $\dsp\lim_{t\to\infty}I(t)=0$.
\end{enumerate}\end{jtheorem}](img448.png)
|
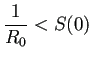 ŃüÉŃéŐšźőŃüĄŃüĘŃüŹŃÇü
ŃüÉŃéŐšźőŃüĄŃüĘŃüŹŃÇü
(ŃüĘŃéŐŃüéŃüłŃüÜ
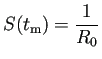 ŃéĺŠ║ÇŃüčŃüÖ
ŃéĺŠ║ÇŃüčŃüÖ ![]() Ńü«ňşśňťĘŃéĺŔ¬ŹŃéüŃéőŃÇé)
Ńü«ňşśňťĘŃéĺŔ¬ŹŃéüŃéőŃÇé) ![]() Ńü»šőşšżęŠŞŤň░ĹÚľóŠĽ░Ńü¬Ńü«Ńüž
Ńü»šőşšżęŠŞŤň░ĹÚľóŠĽ░Ńü¬Ńü«Ńüž
![]() Ńüźň»żŃüŚŃüŽŃÇü
Ńüźň»żŃüŚŃüŽŃÇü
![]() . ŃéćŃüłŃüź
. ŃéćŃüłŃüź
![]() .
ŃéćŃüłŃüź
.
ŃéćŃüłŃüź
![]() ŃüžŃüéŃéőŃüőŃéëŃÇü
ŃüžŃüéŃéőŃüőŃéëŃÇü![]() Ńü»ŠŞŤň░ĹÚľóŠĽ░ŃüžŃüéŃéőŃÇé
Ńü»ŠŞŤň░ĹÚľóŠĽ░ŃüžŃüéŃéőŃÇé
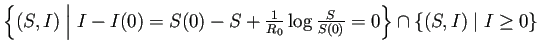 ńŞŐŃüźŔ╝ëŃüúŃüŽŃüäŃéőŃÇé
ŃéćŃüłŃüźŃÇüŃüéŃéő
ńŞŐŃüźŔ╝ëŃüúŃüŽŃüäŃéőŃÇé
ŃéćŃüłŃüźŃÇüŃüéŃéő
![]() Ńü»ňŹśŔ¬┐ŠŞŤň░ĹŃüžŃÇü
Ńü»ňŹśŔ¬┐ŠŞŤň░ĹŃüžŃÇü![]() (
(
![]() ) ŃüžŃüéŃéőŃüőŃéëŃÇü
) ŃüžŃüéŃéőŃüőŃéëŃÇü
![]() ŃüîňşśňťĘŃüÖŃéőŃÇé
ŃüîňşśňťĘŃüÖŃéőŃÇé
![]() Ńé銝ÇňłŁŃü«ŃüćŃüíŃü»ňŹśŔ¬┐ňóŚňŐáŃüĘŃüäŃüćňá┤ňÉłŃééŃüéŃéőŃüîŃÇü
ŃüéŃéőŃüĘŃüôŃéŹŃüőŃéëňůłŃü»ňŹśŔ¬┐ŠŞŤň░ĹŃüźňłçŃéŐŠŤ┐ŃéĆŃéŐŃÇü
ŃéäŃü»ŃéŐ
Ńé銝ÇňłŁŃü«ŃüćŃüíŃü»ňŹśŔ¬┐ňóŚňŐáŃüĘŃüäŃüćňá┤ňÉłŃééŃüéŃéőŃüîŃÇü
ŃüéŃéőŃüĘŃüôŃéŹŃüőŃéëňůłŃü»ňŹśŔ¬┐ŠŞŤň░ĹŃüźňłçŃéŐŠŤ┐ŃéĆŃéŐŃÇü
ŃéäŃü»ŃéŐ ![]() (
(
![]() ) ŃüžŃüéŃéőŃüőŃéëŃÇü
) ŃüžŃüéŃéőŃüőŃéëŃÇü
![]() ŃüîňşśňťĘŃüÖŃéőŃÇé
ŃüîňşśňťĘŃüÖŃéőŃÇé
ň«čŃü»
![]() ŃüÉŃéŐšźőŃüĄŃüôŃüĘŃéĺŔâîšÉćŠ│ĽŃüžŔĘ╝ŠśÄŃüŚŃéłŃüćŃÇé
ŃüÉŃéŐšźőŃüĄŃüôŃüĘŃéĺŔâîšÉćŠ│ĽŃüžŔĘ╝ŠśÄŃüŚŃéłŃüćŃÇé
![]() ŃüĘń╗«ň«ÜŃüÖŃéőŃüĘŃÇü
ŃüéŃéőŠşúŠĽ░
ŃüĘń╗«ň«ÜŃüÖŃéőŃüĘŃÇü
ŃüéŃéőŠşúŠĽ░ ![]() ŃüîňşśňťĘŃüŚŃüŽŃÇü
ŃüÖŃü╣ŃüŽŃü«
ŃüîňşśňťĘŃüŚŃüŽŃÇü
ŃüÖŃü╣ŃüŽŃü«
![]() Ńüźň»żŃüŚŃüŽ
Ńüźň»żŃüŚŃüŽ
![]() .
ŃüôŃéîŃüőŃéë
.
ŃüôŃéîŃüőŃéë
ŃâíŃâó: ňŹüňłćŠÖéÚľôŃüîšÁîÚüÄŃüÖŃéőŃüĘ
![]() ŃüĘŃü¬ŃéőŃüôŃüĘŃü«ŔĘ╝ŠśÄ:
ŔâîšÉćŠ│ĽŃéĺšöĘŃüäŃéőŃÇé
ŃüĘŃü¬ŃéőŃüôŃüĘŃü«ŔĘ╝ŠśÄ:
ŔâîšÉćŠ│ĽŃéĺšöĘŃüäŃéőŃÇé
![]() (
(![]() ) ŃüĘń╗«ň«ÜŃüÖŃéőŃüĘŃÇü
) ŃüĘń╗«ň«ÜŃüÖŃéőŃüĘŃÇü
![]() .
ŃéćŃüłŃüź
.
ŃéćŃüłŃüź
![]() . ŃüôŃéîŃüőŃéë
. ŃüôŃéîŃüőŃéë
![]() . ŃéćŃüłŃüź
. ŃéćŃüłŃüź
![]() .
ŃüôŃéîŃü»
.
ŃüôŃéîŃü»
![]() Ńüʚ荚ŤżŃüÖŃéőŃÇé
Ńüʚ荚ŤżŃüÖŃéőŃÇé
ń╗ąńŞőŃü« (6.9) ŃüĘŃüäŃü抾╣šĘőň╝ĆŃéĺŠÄ▓ŃüĺŃüŽŃüäŃéőŠťČŃééňĄÜŃüäŃü«ŃüžŃÇü ňĽĆŃüźŃüŚŃüŽŃüŐŃüĆŃÇé
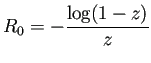 |
(6.7) |
Šíéšö░ šąÉňĆ▓