Next: 6.4 ТЋ░тГдуџёУДБТъљ (2) уёАТгАтЁЃтїќсЂетЪ║ТюгтєЇућЪућБТЋ░ Up: 6 SIRсЃбсЃЄсЃФ Previous: 6.2 ТЋ░тђцсѓисЃЪсЃЦсЃгсЃ╝сѓисЃДсЃ│
ТЋ░тГдуџёУДБТъљсѓѓсЂЌсЂдсЂ┐сѓѕсЂєсђѓ сѓёсЂБсЂдсЂ┐сѓІсЂесђЂLotka-Volterra Тќ╣уеІт╝ЈсЂ«ТЎѓсЂетљїсЂўсѓѕсЂєсЂфсЂесЂЊсѓЇсѓѓтцџсЂёсђѓ
Lotka-Volterra сЂ«Тќ╣уеІт╝ЈсЂ«та┤тљѕсЂетљїТДўсЂФсђЂ
т▒ђТЅђУДБсЂ«тГўтюесђЂУДБсЂ«СИђТёЈТђДсЂ»сЂЎсЂљтѕєсЂІсѓІ (у░АтЇўсЂфсЂ«сЂДуюЂуЋЦсЂЎсѓІ)сђѓ
сЂЙсЂЪУДБсЂї
![]() тЁеСйЊсЂФт╗ХжЋисЂДсЂЇсѓІсЂЊсЂесѓѓтљїТДўсЂФсЂЌсЂдУе╝ТўјсЂїсЂДсЂЇсѓІ
(С╗ЦСИІсЂДуц║сЂЎсѓѕсЂєсЂФУДБУ╗їжЂЊсЂ«Тќ╣уеІт╝ЈсЂїТ▒ѓсЂЙсѓІсЂ«сЂДсђЂ
сЂЮсѓїсЂІсѓЅУДБсЂ«ТюЅуЋїТђДсЂ«УГ░УФќсѓњухїсЂдУе╝ТўјсЂДсЂЇсѓІ)сђѓ
тЁеСйЊсЂФт╗ХжЋисЂДсЂЇсѓІсЂЊсЂесѓѓтљїТДўсЂФсЂЌсЂдУе╝ТўјсЂїсЂДсЂЇсѓІ
(С╗ЦСИІсЂДуц║сЂЎсѓѕсЂєсЂФУДБУ╗їжЂЊсЂ«Тќ╣уеІт╝ЈсЂїТ▒ѓсЂЙсѓІсЂ«сЂДсђЂ
сЂЮсѓїсЂІсѓЅУДБсЂ«ТюЅуЋїТђДсЂ«УГ░УФќсѓњухїсЂдУе╝ТўјсЂДсЂЇсѓІ)сђѓ
|
|
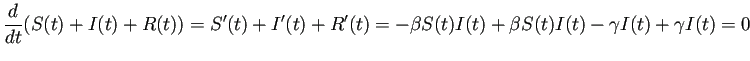
уиЈС║║тЈБсЂ»т«џТЋ░сЂДсЂѓсѓІсЂІсѓЅсђЂсЂЊсѓїсѓњ ![]() сЂесЂЎсѓІсЂесЂЇсђЂ
сЂесЂЎсѓІсЂесЂЇсђЂ
| (6.2) |
SIRсЃбсЃЄсЃФсЂ«ТюђтѕЮсЂ«2сЂцсЂ«Тќ╣уеІт╝Ј
| (6.4) |
![\begin{jtheorem}
% latex2html id marker 1249
\begin{enumerate}[(1)]
\item
$(S...
...ђЂУ▓асЂ«жЃетѕєсЂ»сЂЮсѓїсЂъсѓїУДБУ╗їжЂЊсЂДсЂѓсѓІсђѓ
\end{enumerate}\end{jtheorem}](img398.png)
|
![\begin{jtheorem}[SIRсЃбсЃЄсЃФсЂ«УДБсЂ«ТђДУ│ф]
тѕЮТюЪтђц $(S(0),I(0))$\ сЂї $S(0...
...$S=\frac{\gamma}{\beta}$\ сЂДТюђтцДтђцсѓњтЈќсѓІсђѓ
\end{enumerate}\end{jtheorem}](img399.png)
|
уЅ╣сЂФсђЂ
![]() сЂфсѓЅсЂ░сђЂ
сЂфсѓЅсЂ░сђЂ
![]() сЂ»
сЂ» ![]() сЂ«жќбТЋ░сЂесЂЌсЂдуІГуЙЕсЂ«тбЌтіажќбТЋ░сђЂ
ТЎѓтѕ╗
сЂ«жќбТЋ░сЂесЂЌсЂдуІГуЙЕсЂ«тбЌтіажќбТЋ░сђЂ
ТЎѓтѕ╗ ![]() сЂ«жќбТЋ░сЂесЂЌсЂдуІГуЙЕсЂ«ТИЏт░ЉжќбТЋ░сЂДсЂѓсѓІсђѓ
сЂ«жќбТЋ░сЂесЂЌсЂдуІГуЙЕсЂ«ТИЏт░ЉжќбТЋ░сЂДсЂѓсѓІсђѓ
![]() сЂфсѓЅсЂ░сђЂ
сЂфсѓЅсЂ░сђЂ![]() сЂїт░ЈсЂЋсЂё (
сЂїт░ЈсЂЋсЂё (
![]() сЂїТѕљсѓіуФІсЂц) сЂєсЂАсЂ»сђЂ
сЂїТѕљсѓіуФІсЂц) сЂєсЂАсЂ»сђЂ![]() сЂ»тбЌтіажќбТЋ░сЂДсђЂ
сЂ»тбЌтіажќбТЋ░сЂДсђЂ
![]() сЂїтцДсЂЇсЂё (
сЂїтцДсЂЇсЂё (
![]() сЂїТѕљсѓіуФІсЂц) сЂесЂЇсЂ»сђЂ
сЂїТѕљсѓіуФІсЂц) сЂесЂЇсЂ»сђЂ
![]() сЂ»ТИЏт░ЉжќбТЋ░сЂДсЂѓсѓІсђѓ
сЂ»ТИЏт░ЉжќбТЋ░сЂДсЂѓсѓІсђѓ
сЂЊсЂ«т«џуљєсЂ«Уе╝ТўјсЂ»сђЂ сЂ╗сЂЕсЂ╗сЂЕсЂ«жЏБсЂЌсЂЋсЂДсЂѓсѓЇсЂєсђѓ сЂесЂёсЂєсЂЊсЂесЂДсђЂТ╝ћу┐њУф▓жАїсЂФсЂЌсЂдсЂёсЂЪсЂ«сЂасЂЉсѓїсЂЕсђЂ Уф░сѓѓУДБсЂёсЂдсЂЈсѓїсЂфсЂёсЂ«сЂДсђЂС╗ЦСИІсЂФУе╝Тўјсѓњуц║сЂЎсђѓ
сѓѓсЂєт░ЉсЂЌУЕ│сЂЌсЂЈсЂёсЂєсЂесђЂугг1У▒АжЎљсЂ«уѓ╣ ![]() сЂІсѓЅтЄ║уЎ║сЂЌсЂЪУДБ
(тѕЮТюЪТЮАС╗Х
сЂІсѓЅтЄ║уЎ║сЂЌсЂЪУДБ
(тѕЮТюЪТЮАС╗Х
![]() сѓњТ║ђсЂЪсЂЎтЙ«тѕєТќ╣уеІт╝ЈсЂ«УДБ) сЂїсђЂ
угг1У▒АжЎљсЂ«УБюжЏєтљѕсЂФтѕ░жЂћсЂЎсѓІсЂфсѓЅсЂ░сђЂ
СИГжќЊтђцсЂ«т«џуљєсЂФсѓѕсЂБсЂдсђЂ
сѓњТ║ђсЂЪсЂЎтЙ«тѕєТќ╣уеІт╝ЈсЂ«УДБ) сЂїсђЂ
угг1У▒АжЎљсЂ«УБюжЏєтљѕсЂФтѕ░жЂћсЂЎсѓІсЂфсѓЅсЂ░сђЂ
СИГжќЊтђцсЂ«т«џуљєсЂФсѓѕсЂБсЂдсђЂ
![]() У╗ИСИісЂ«уѓ╣
У╗ИСИісЂ«уѓ╣
![]() (сЂЊсЂЊсЂД
(сЂЊсЂЊсЂД
![]() ) сЂІсђЂ
) сЂІсђЂ
![]() У╗ИСИісЂ«уѓ╣
У╗ИСИісЂ«уѓ╣
![]() (сЂЊсЂЊсЂД
(сЂЊсЂЊсЂД ![]() ) сѓњжђџсѓІсђѓ
сЂЎсЂфсѓЈсЂАсђЂсЂѓсѓІ
) сѓњжђџсѓІсђѓ
сЂЎсЂфсѓЈсЂАсђЂсЂѓсѓІ
![]() сЂїтГўтюесЂЌсЂд
сЂїтГўтюесЂЌсЂд
![]() сЂЙсЂЪсЂ»
сЂЙсЂЪсЂ»
![]() .
тЅЇУђЁсЂ«та┤тљѕсђЂ
.
тЅЇУђЁсЂ«та┤тљѕсђЂ![]() У╗ИСИісЂ«уѓ╣сЂїт╣│УААуѓ╣сЂДсЂѓсѓІсЂЊсЂесЂІсѓЅсђЂУДБсЂ«СИђТёЈТђДсЂФтЈЇсЂЎсѓІсђѓ
сЂЙсЂЪтЙїУђЁсЂФсЂцсЂёсЂдсЂ»сђЂ
У╗ИСИісЂ«уѓ╣сЂїт╣│УААуѓ╣сЂДсЂѓсѓІсЂЊсЂесЂІсѓЅсђЂУДБсЂ«СИђТёЈТђДсЂФтЈЇсЂЎсѓІсђѓ
сЂЙсЂЪтЙїУђЁсЂФсЂцсЂёсЂдсЂ»сђЂ
![]() сЂїУДБсЂДсЂѓсѓІсЂЊсЂесЂІсѓЅсђЂ
сѓёсЂ»сѓіУДБсЂ«СИђТёЈТђДсЂФтЈЇсЂЎсѓІсђѓ
сѓєсЂѕсЂФугг1У▒АжЎљтєЁсЂ«уѓ╣сЂІсѓЅтЄ║уЎ║сЂЌсЂЪУДБсЂ»угг1У▒АжЎљтєЁсЂФсЂесЂЕсЂЙсѓІсђѓ
сЂїУДБсЂДсЂѓсѓІсЂЊсЂесЂІсѓЅсђЂ
сѓёсЂ»сѓіУДБсЂ«СИђТёЈТђДсЂФтЈЇсЂЎсѓІсђѓ
сѓєсЂѕсЂФугг1У▒АжЎљтєЁсЂ«уѓ╣сЂІсѓЅтЄ║уЎ║сЂЌсЂЪУДБсЂ»угг1У▒АжЎљтєЁсЂФсЂесЂЕсЂЙсѓІсђѓ
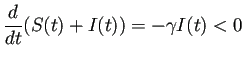
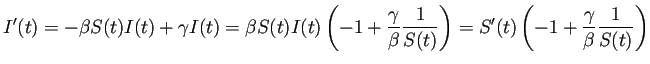
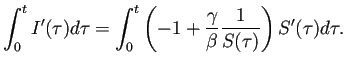
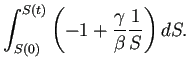
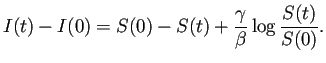
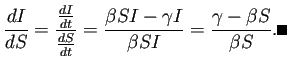
ТАѓућ░ уЦљтЈ▓