6.2 数値シミュレーション

実は SIR モデルの厳密解が求まるという話があるが (Harko-Lobo-Mak [23])、 あまり使いやすい式ではないそうである。

ここでは数値シミュレーションをしてみる。 ほとんど Lotka-Volterra 方程式と同様に扱うことができる。 Lotka-Volterra の方程式のプログラムがあれば、 それをたたき台にしてプログラムを作ることは簡単で良い練習課題である。

桂田 [4] の 付録G「専用の関数を使ってみる - Python, Julia」 に Python によるプログラムがある。

図 7: 無次元化SIRモデルと4つの可視化 $R_0=2.5$ (桂田 [4])

$S$,$I$,$R$の時間変化, 2次元解軌道, 流行曲線, 3次元解軌道

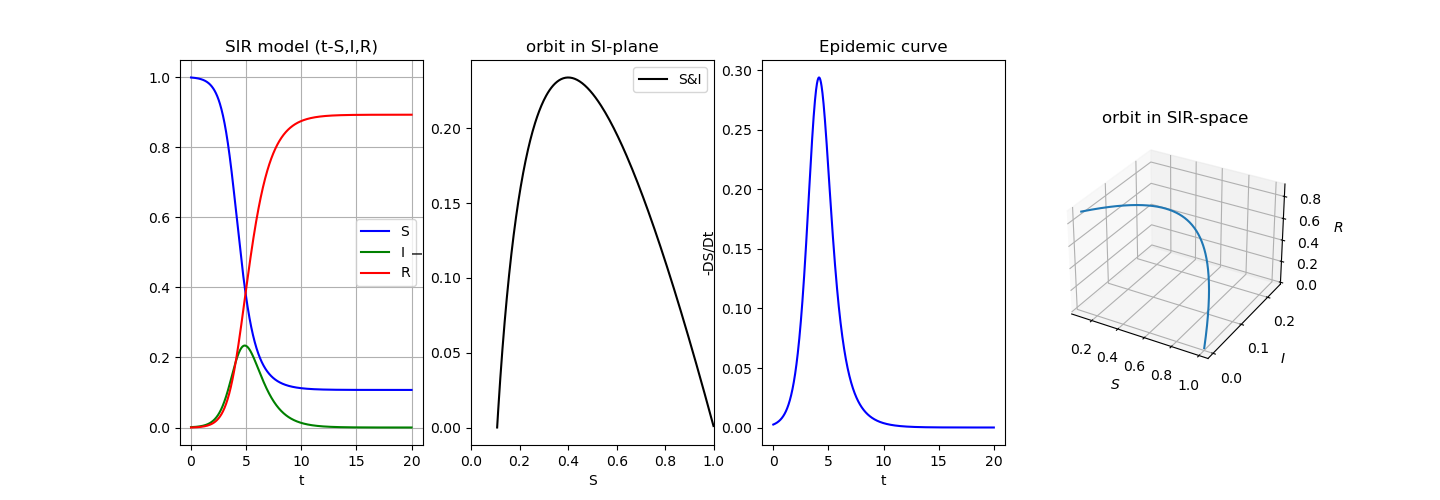
神永 [22] の§5.2 にも Python のプログラムが載っている。 [22] では、さらに SIRモデルを改良した SEIR モデルを用いて、 COVID-19 の日本における第一波のシミュレーションを行い、 実データと比較対照している。