D..3 解の存在範囲 (爆発, 極大延長解)

前項の定理で、 $\delta$ という範囲を制限するものが出て来てしまったが、 これは仕方がないことである。

注: 実は有名な logistic 方程式でも解の爆発はおこる (本文中に解の存在範囲が限定されることを説明した)。 実際の現象とは関わりがない場合 (初期値が負であったり、 環境収容力より大きかったり) なので、普通は問題とされないが。 $\qedsymbol$

爆発が起らないための十分条件としては、 次のリプシッツ条件が 有名である²³。

$x$ に関する Lipschitz 条件

   $$\mbox{定数 $L$\ が存在して}$$$$\quad \vert f(t,x_1)-f(t,x_2)\vert\le L \vert x_1-x_2\vert.$$

特に $f(t,x)$ が $x$ の $1$ 次関数 ( $f(t,x)=A(t)x+b(t)$ という形) である場合 (言い換えると線形微分方程式の場合) は、 ごく緩い仮定 (例えば $A(t)$ が有界) の下でリプシッツ条件が成り立つ (したがって解の爆発は起らない)。

爆発が起らない場合は、 解は方程式が意味を持つ ($f$ の定義域をはみ出ない) 範囲で存在することが知られている。 これについて、以下なるべく簡潔な説明を試みる。

$D$ を $\mathbb{R}\times\mathbb{R}^n$ の領域または閉領域とする ²⁴。 $f\colon D\to\mathbb{R}^n$ は連続で、微分方程式

を課した初期値問題について考える。

以下、 初期値問題 (F.4), (F.2) の解とは、 その定義域が $t_0$ を左端とする区間 $I$ で、初期条件 $x(t_0)=x_0$ と、 $I$ 全体で微分方程式を満たすような関数 $x(t)$ のことをいう。 また、$I$ のことを解 $x(t)$ の定義区間と呼ぶことにする。

初期時刻 $t_0$ の 十分近く (ある正の数 $\delta$ に対して、 $t\in[t_0-\delta,t_0+\delta]$ を満たす範囲) では解 (局所解) が存在する、という定理があるわけだが、 それだけでは満足できない。出来る限り広い範囲での解の存在を保証してほしい。

ここではまず素朴な検討をしてみる。新たな初期値問題

$$\frac{\D y}{\D t}=f(t,x)$$
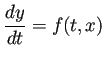に初期条件

$$y(t_0+\delta)=x(t_0+\delta)$$

を考えることで、 もう少し先まで ( $[t_0,t_0+\delta+\delta']$ まで) 解を延ばすことができる。 つまり $y$ が $[t_0+\delta-\delta',t_0+\delta+\delta']$ で定義されているとき、

$$\widetilde x(t) := \left\{ \begin{array}{ll} x(t)& \text{($t\... ...\ y(t)& \text{($t\in(t_0+\delta,t_0+\delta+\delta']$)} \end{array} \right\}$$

定めた $\widetilde x$ は、 初期値問題 (F.4), (F.2) の解である。

ちょっと考えると、これを続けることで、 どこまでも解を延ばすことが出来そうだが、 有限の限界 $T$ があるかもしれない ( $t_0+\delta+\delta'+\delta''+\cdots=T<+\infty$ -- 正の数を足し続けても、 限りなく増えるわけではない)。

(F.4), (F.2) の解のうち、 真に大きな定義区間が存在しないような(それ以上延ばせない)解のことを、 (F.4), (F.2) の極大延長解と呼ぶことにする。 例えば

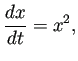$$\frac{\D x}{\D t}=x^2,$$ (D.2)

$$x(0)=a$$ (D.3)

の場合、 $x(t)=\dfrac{1}{1/a-t}$ ( $-\infty<t<1/a$) は極大延長解である。

微分方程式の初期値問題の解の一意性が成り立つ場合 (例えば $x$ について局所 Lipschitz 条件が成り立つ) には、 極大延長解を構成するという方針で、 極大延長解の存在が証明できる (例えば高野 [40] の§5.3)。 この場合は最大延長解と呼ぶ方が適切かもしれない。

簡単のため、以下の議論では解の一意性が成り立つことを仮定する。

いくつかのテキストで、次のように説明されている。

「極大延長解 $x(t)$ ( $t_0\le t<T$ あるいは $t_0\le t\le T$) は、 $t\to T$ のとき $x(t)$ が有界でないか、$f$ の定義域 $D$ の境界に近づく」

これを用いると、解 $x(t)$ が有界であることを示せば、 解が $D$ の境界に近づくことが分かる。 これは満足すべき状況に思えるかもしれない。

しかし $D$ の境界に近づくとは、正確にはどういう意味であろうか。 正直なことを言うと、私にはよく分からない ($t\to T$ のとき、$x(t)$ は有界であるが、振動し、 $x(t)$ は境界から離れたり近づいたりすることがありそうに思われる)。 定義を明記してあるテキストを見た覚えがない (単に私が不勉強なだけかもしれないが…)。 定義を書いていないということは、証明もきちんとは書かれていないことを意味する。

仕方がないので、私自身は、次のことを使っている。

極大延長解のグラフ上で $f$ が有界ならば、 $x_T:=\dsp\lim_{t\to T} x(t)$ が存在して、 $(T,x_T)$ は $D$ の境界点である (すなわち ( $\forall\eps>0$) $B((T,x_T);\eps)$ は $D$ と $D^\complement$ の両方と交わる)。

証明には、次の二つの定理を用いる。

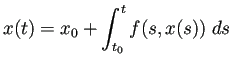(この2つの定理は、関数が初期値問題の解であることと、 積分方程式 $x(t)=x_0+\dsp\int_{t_0}^t f(s,x(s))\;\D s$ の解であることが同値であること(これは常識的)を用いれば証明できる。 難しくないが証明は省略する。例えば桂田 [41] を見よ。 これは、 コディントン・レヴィンソン [30] を参考にして考えたことをメモしたものなので、 直接 [30] を見る方が良いかもしれない。)

極大延長解の場合に、もしも $(T,x_T)$ が $D$ の内点であれば、 初期条件 $x(T)=x_T$ の初期値問題を考えることで、 解が $T$ を超えて延長できることが導かれ、矛盾が生じる。 ゆえに $(T,x_T)$ は $D$ の境界点である。