Next: D..5 сЂЙсЂесѓЂ Up: D. тѕЮТюЪтђцтЋЈжАїсЂ«тЪ║уцјуљєУФќ (сЂІсЂЉУХ│сЂДУфгТўј) Previous: D..3 УДБсЂ«тГўтюеу»ётЏ▓ (уѕєуЎ║, ТЦхтцДт╗ХжЋиУДБ)
тИИтЙ«тѕєТќ╣уеІт╝ЈсЂ«тѕЮТюЪтђцтЋЈжАїсЂ«УДБсЂ«тГўтюесЂїтѕєсЂІсЂБсЂЪсЂесЂЌсЂдсђЂ сЂцсЂјсЂФТ░ЌсЂФсЂфсѓІсЂ«сЂ»сђЂУДБсЂїсЂЪсЂаСИђсЂцсЂФжЎљсѓІсЂІсЂесЂёсЂєсЂЊсЂесЂДсЂѓсѓІсђѓ
тѕЮТюЪтђцтЋЈжАї
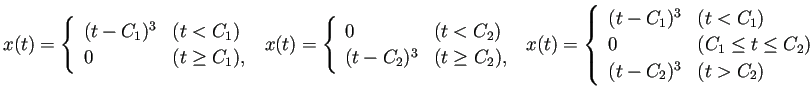
сЂЮсЂЊсЂДУДБсЂ«СИђТёЈТђДсѓњС┐ЮУе╝сЂЎсѓІТЮАС╗ХсЂїуЪЦсѓісЂЪсЂЈсЂфсѓІсЂїсђЂТгАсЂ«т«џуљєсЂїжЮътИИсЂФТюЅтљЇсЂДсЂѓсѓІсђѓ (сЂЌсЂІсЂЌсђЂт┐юућеСИісЂ»сЂЮсЂ«ТгАсЂ«т«џуљєD.9 сЂїСЙ┐тѕЕсЂфсЂ«сЂДсђЂ сѓѓсЂЌсѓѓ1сЂцсЂасЂЉУдџсЂѕсѓІсЂфсѓЅсЂ░сђЂ т«џуљєD.9сѓњУдџсЂѕсѓІсЂЊсЂесѓњтІДсѓЂсѓІсђѓ)
![\begin{jlemma}[сЃфсЃЌсѓисЃЃсЃёТЮАС╗ХсѓњсЂ┐сЂЪсЂЎта┤тљѕсЂ«СИђТёЈТђД]
жђБуХџжќбТЋ...
...]$, $b_\ast:=\min\{b_1,b_2\}$)}
\end{displaymath}сЂїТѕљсѓіуФІсЂцсђѓ
\end{jlemma}](img719.png)
|
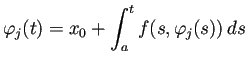
![$\displaystyle \psi(t)=\int_a^t \left[f(s,\varphi_1(s))-f(s,\varphi_2(s))\right]\,\D s
$](img724.png)
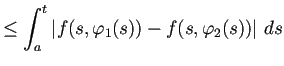 |
||
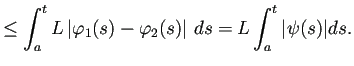 |
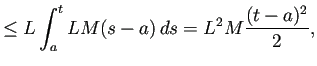 |
||
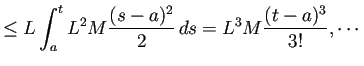 |
![$\displaystyle \vert\psi(t)\vert\le M\frac{\left[L(t-a)\right]^n}{n!}
\le M\frac{\left[L(b_\ast-a)\right]^n}{n!}$](img733.png)
тИИтЙ«тѕєТќ╣уеІт╝ЈсЂ«тѕЮТюЪтђцтЋЈжАїсЂ«та┤тљѕсђЂ
СИђТёЈТђДсЂїТѕљсѓіуФІсЂцсЂесЂёсЂєсЂ«сЂ»УДБсЂїТъЮтѕєсЂІсѓїсѓњсЂЌсЂфсЂёсЂЊсЂесЂДсЂѓсѓІсЂІсѓЅсђЂ
СИђТёЈТђДсѓњС┐ЮУе╝сЂЎсѓІсЂФсЂ» Lipschitz ТЮАС╗ХсЂ»т▒ђТЅђуџёсЂфсѓѓсЂ«сЂДтЇЂтѕєсЂДсЂѓсѓі
(сЂцсЂЙсѓі ![]() сЂ»тЁеСйЊсЂДух▒СИђуџёсЂФтЈќсѓїсЂфсЂЈсЂдсѓѓТДІсѓЈсЂфсЂё)сђЂ
СЙІсЂѕсЂ░
сЂ»тЁеСйЊсЂДух▒СИђуџёсЂФтЈќсѓїсЂфсЂЈсЂдсѓѓТДІсѓЈсЂфсЂё)сђЂ
СЙІсЂѕсЂ░ ![]() сЂї
сЂї ![]() у┤џсЂДсЂѓсѓїсЂ░сѓѕсЂёсЂЊсЂесЂїтѕєсЂІсѓІсђѓ
сЂЎсЂфсѓЈсЂАТгАсЂїТѕљуФІсЂЎсѓІ (т┐юућеСИісЂесЂдсѓѓСЙ┐тѕЕсЂфсЂ«сЂДсЂюсЂ▓УдџсЂѕсЂдсЂісЂЊсЂє)сђѓ
у┤џсЂДсЂѓсѓїсЂ░сѓѕсЂёсЂЊсЂесЂїтѕєсЂІсѓІсђѓ
сЂЎсЂфсѓЈсЂАТгАсЂїТѕљуФІсЂЎсѓІ (т┐юућеСИісЂесЂдсѓѓСЙ┐тѕЕсЂфсЂ«сЂДсЂюсЂ▓УдџсЂѕсЂдсЂісЂЊсЂє)сђѓ
![\begin{jtheorem}[$C^1$\ у┤џсЂфсѓЅсЂ░СИђТёЈТђДсЂїТѕљуФІ]
$f$\ сЂї $C^1$\ у┤џсЂ«ж...
..., $b_\ast:=\min\{b_1,b_2\}$)}
\end{displaymath}сЂїТѕљсѓіуФІсЂцсђѓ
\end{jtheorem}](img738.png)
|
СИісЂ«СЙІсЂ«
![]() сЂДсЂ»сђЂ
сЂДсЂ»сђЂ![]() сЂД
сЂД ![]() сЂ»тЙ«тѕєтЈ»УЃйсЂДсЂфсЂЈ
(тЙЊсЂБсЂд
сЂ»тЙ«тѕєтЈ»УЃйсЂДсЂфсЂЈ
(тЙЊсЂБсЂд ![]() у┤џсЂДсѓѓсЂфсЂЈ)сђЂ
Lipschitz ТЮАС╗Хсѓѓ 0 сЂ«сЂесЂЊсѓЇсЂДт┤ЕсѓїсЂдсЂёсѓІсЂЊсЂесЂФТ│еТёЈсЂЌсѓѕсЂєсђѓ
у┤џсЂДсѓѓсЂфсЂЈ)сђЂ
Lipschitz ТЮАС╗Хсѓѓ 0 сЂ«сЂесЂЊсѓЇсЂДт┤ЕсѓїсЂдсЂёсѓІсЂЊсЂесЂФТ│еТёЈсЂЌсѓѕсЂєсђѓ