2.5.2 Runge-Kutta法

常微分方程式の初期値問題の数値解法のうち、 比較的簡単で、高精度な解が得られるため、良く用いられる方法として ⁸、 次の Runge-Kutta法 (4次のRunge-Kutta法, 古典的Runge-Kutta法とも呼ばれる) がある。 これは次の漸化式で $\{x_n\}$ を定めるものである。

$$% 2022-02-8 14:32の式群 \begin{equation}x_{n+1}=x_n+\frac{1}{6... ...n+1}=x_n+\frac{1}{6}\left(k_{1,n}+2k_{2,n}+2k_{3,n}+k_{4,n}\right). \end{align}$$

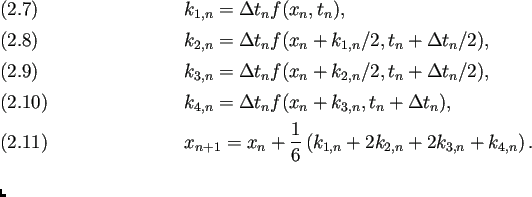Euler法にせよ、Runge-Kutta 法にせよ、 多くの場合 $t_n$ は等分点に取る。つまり $[t_0,T]$ を $N$ 等分するとして

$$\Delta t:=\frac{T-t_0}{N},\quad t_n:=t_0+n\Delta t$$   ( $n=1,2,\cdots,N$)

で定める ( $\Delta t_n\equiv \Delta t$ ということ)⁹。

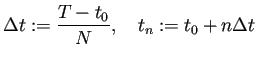以下この節では、特に断りのない限り、 解こうとしている区間 $[t_0,T]$ を $N$ 等分する場合を考えることにする。

C プログラマー向けの説明    

「常微分方程式の初期値問題を解くプログラムの書き方 §2 Euler法, Runge-Kutta法入門 -- 1次元の問題」 の §2.3.2 Runge-Kutta法のCプログラム例 で、C言語によるプログラム例が見られる。

runge-kutta.c

/*
 * runge-kutta.c (Runge-Kutta method for Malthusian model)
 */

#include <stdio.h>

double a = 1.0;

int main(void)
{
  int i, N;
  double t, x, dt, k1, k2, k3, k4;
  double f(double, double), x0;
  double Tmax;
  // 初期値
  x0 = 1.0;
  // 最終時刻
  Tmax = 1.0;
  // 時間刻み
  printf("# N: "); scanf("%d", &N);
  dt = Tmax / N;
  // 初期値
  t = 0.0;
  x = x0;
  printf("# t x\n");
  printf("%f %f\n", t, x);
  // Runge-Kutta 法
  for (i = 0; i < N; i++) {
    k1 = dt * f(x, t);
    k2 = dt * f(x + k1/2, t + dt / 2);
    k3 = dt * f(x + k2/2, t + dt / 2);
    k4 = dt * f(x + k3, t + dt);
    x += (k1 + 2 * k2 + 2 * k3 + k4) / 6;
    t = (i + 1) * dt;
    printf("%f %20.14f\n", t, x);
  }
  return 0;
}

double f(double x, double t)
{
  return a * x;
}

解曲線の図を描くための手順は Euler 法のときと同様 (データファイルの名前を変えるくらい) なので省略する。

必修課題 2.5.2   上のプログラムを実行して、解のグラフ (解曲線) を描いてみよ。

必修課題 2.5.3   $a=1$, $x_0=1$, $t_0=0$, $T=1$ とし、初期値問題 (F.6a), (F.6b) を、 $[t_0,T]$ を $N$分割して、 Euler法、Runge-Kutta 法で解いたときの計算精度を調べよ。 $N$ が増加するにつれて (例えば $N=10,100,1000,10000,\cdots$ で計算してみる)、 どのように変化するか (図2 も見てみよう)。

$x_N$ は $x(1)=x_0 e^{a(T-t_0)}=1\cdot e^{1(1-0)}=e =2.7182818284\cdots$ の近似であることを用いる。

以下の2つの課題は、プログラムとは直接の関係はなく、紙の上の数学の問題である。

課題 2.5.1   $a=1$, $x_0=1$, $t_0=0$, $T=1$ とし、 $[t_0,T]$ を $N$分割して、 (F.6a), (F.6b) を (前進) Euler法、(後退) Euler法で解いた場合の $x_N$ を文字式 ($\Delta t$ を用いる) で表せ。その結果の妥当性を説明せよ。

(ヒント: 高校の数学IIIで学んだ $\dsp\lim_{x\to 0}\left(1+x\right)^{1/x} =e$ を思い出すと、 $N\to+\infty$ のとき $x_N$ が真の解に収束することが納得できるはず。 )

課題 2.5.2   $a=1$, $x_0=1$, $t_0=0$, $T=1$ の場合に (F.6a), (F.6b) を (前進) Euler法、Runge-Kutta法で解いた場合の $x_1$ を文字式 ($\Delta t$ を用いる) で表すと、それぞれ $1+\Delta t$, $1+\Delta t+\frac{(\Delta t)^2}{2}+\frac{(\Delta t)^3}{6}+ \frac{(\Delta t)^4}{24}$ となることを示せ。 これから $x(t_1)$ と $x_1$ の差がそれぞれ $O\left((\Delta t)^2\right)$, $O\left((\Delta t)^5\right)$ であることを説明せよ。

Euler法、Runge-Kutta法の次数という重要な概念に触れるために、 次の研究課題に取り組むことを勧める。

研究課題 2.5.1   $a=1$, $x_0=1$, $t_0=0$, $T=1$ の場合に (F.6a), (F.6b) を (前進) Euler法、Runge-Kutta法で解くプログラムを作り (プログラミング言語は何でもよい)、 $N$ を $10$, $20$, $40$, $\cdots$ に対して $x_N$ を求めて、 $x(T)-x_N$ が $O(N^{-1})$, $O(N^{-4})$ であることを示せ (横軸 $N$, 縦軸 $\left\vert x(T)-x_N\right\vert$ で両側対数プロットをすること)。

図 2: Euler法とRunge-Kutta法の精度の比較

この図2 をどうやって描いたか、 付録 H.2 (p. ) に説明してある。

C プログラマー向けの説明     上の runge-kutta.c の Python バージョンは次のようになる。

runge-kutta.py

# runge-kutta.py --- Malthus方程式をRunge-Kutta法で解く
# Cプログラムの Python バージョン
# runge-kutta.c(http://nalab.mind.meiji.ac.jp/~mk/labo/text/ode-workbook/node11.html)
# Runge-Kutta法であるが、応用が効きにくい形。参考プログラム。

def f(x, t):
    return a * x

a=1
x0=1
Tmax=1
str=input('N='); N=int(str);
dt=Tmax/N

t=0.0; x=x0
print('%f %f' % (t,x))
for i in range(N):
    k1 = dt * f(x,t)
    k2 = dt * f(x + k1/2, t + dt / 2)
    k3 = dt * f(x + k2/2, t + dt / 2)
    k4 = dt * f(x + k3, t + dt)
    x += (k1 + 2 * k2 + 2 * k3 + k4) / 6
    t = (i + 1) * dt
    print('%f %f' % (t,x))

このプログラムを色々書き換えてみよう。

• 解曲線を描くように。 タイトルをつけたり、グリッドを描いたり、 描画範囲を $0\le t\le 1$, $0\le x\le 3$ にしたり、 座標軸を描いたり、軸ラベルをつけてみたり。
• 誤差 $x(t_N)-x_N=e-x_N$ の値を表示するように。