解の公式 (G.3) を認めれば、
次のことが成り立つのは容易に分かる。
- (a)
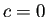 ならば、任意の
ならば、任意の
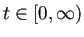 に対して
に対して 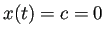 .
.
- (b)
-
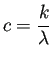 ならば、任意の
ならば、任意の
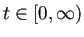 に対して
に対して
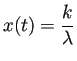 .
.
研究課題 3.3.1
「
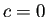
のとき、
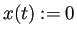
(
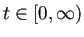
) とおくと、
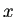
は logistic equation (
C.22) と初期条件を
満たすことは簡単に確かめられる。」この説明を (a) の証明とするには、
微分方程式の初期値問題の解の一意性についての定理が必要である。
どういう定理か説明し、それを用いて (a) の証明を完成させよ。
この事実 (a), (b) を、
「0 と
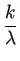 は、
(C.22) の平衡点
(equilibrium10point, 平衡解) である」と言う。
は、
(C.22) の平衡点
(equilibrium10point, 平衡解) である」と言う。
必修課題 3.3.1 (常微分方程式の力学系の)
平衡点の定義を調べて説明せよ。
(付録G.4 に書いておいたので、
それを読んで理解すれば良い。)
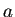 が微分方程式
が微分方程式
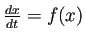 の平衡点であるとき、
の平衡点であるとき、
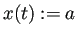
(
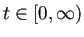
)
とおくと、これは微分方程式の解であることを示せ。
解の公式 (G.3) を認めれば、
次のことも容易に分かる。
- (i)
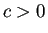 ならば、
ならば、
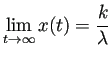 .
.
- (ii)
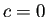 ならば、
ならば、
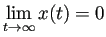 .
.
- (iii)
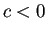 ならば、
ならば、
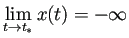 .
.
このことから次のことが分かる。
- (A)
- 平衡点
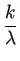 は漸近安定である。
は漸近安定である。
- (B)
- 平衡点 0 は不安定である。
必修課題 3.3.3
平衡点に対する「安定」、「漸近安定」、「不安定」という用語の定義を調べて、
上の (A), (B) が正しいことを示せ。
(やはり付録G.4 に書いておいたので、
それを読んで理解してから取り組むこと。)
図 3:
P. F. Verhulst, Notice sur la loi que la population suit
dans son accroissement, Correspondance mathématique et physique,
Vol. 10, pp. 113-121 (1838) の p. 115. 最近は、
多くの原典がネットで少し探しただけで見つけられる。
OCRされていれば、
機械翻訳 (DeepL翻訳, Google 翻訳等) にかけて日本語訳を得るのも簡単である。
せっかく便利なものが使えるようになったのだから、
こまめに検索・調査することを勧める。
(2023/7追記) macOS Ventura から、画像ファイルからでも、
OCRによるテキスト情報のコピー&ペーストができるようになった。
|
 |
念のため: DeepL翻訳 https://www.deepl.com/ja/translator
桂田 祐史
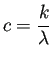 ならば、任意の
ならば、任意の
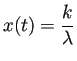 .
.
![]() は、
(C.22) の平衡点
(equilibrium10point, 平衡解) である」と言う。
は、
(C.22) の平衡点
(equilibrium10point, 平衡解) である」と言う。
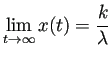 .
.
