Next: G..5 復習: 定数係数線形常微分方程式 Up: G. 力学系についてのメモ Previous: G..3 平衡点の安定性、漸近安定性
(G.1) の平衡点 ![]() の安定性の判定法として、
次の定理が使われることが非常に多い。
の安定性の判定法として、
次の定理が使われることが非常に多い。

|
「ヤコビ行列って何ですか?」
(学生が持っている教科書の索引にヤコビ行列がない…ぶつぶつ )
![]() ,
,
![]() ,
,
![]() は微分可能とするとき、
は微分可能とするとき、
![]() の
の ![]() におけるヤコビ行列とは、
におけるヤコビ行列とは、![]() 型の
行列
型の
行列
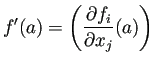
力学系
![]() においては
においては ![]() であることに注意しよう
(微分方程式の左辺は
であることに注意しよう
(微分方程式の左辺は ![]() 次元, 右辺は
次元, 右辺は ![]() 次元で、それが一致するから)。
ゆえに
次元で、それが一致するから)。
ゆえに ![]() は
は ![]() 次正方行列で、
(重複度を込めて数えて)
次正方行列で、
(重複度を込めて数えて) ![]() 個の固有値を持つ。
行列
個の固有値を持つ。
行列 ![]() の成分は実数であるが、固有値には虚数が現れることもある。
の成分は実数であるが、固有値には虚数が現れることもある。
この定理が、![]() の場合にも使えることを注意しておく。
の場合にも使えることを注意しておく。
![]() のとき、
のとき、![]() の
の ![]() におけるヤコビ行列は、
におけるヤコビ行列は、
![]() の
の ![]() における微分係数
における微分係数
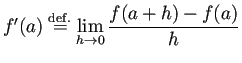 そのものである。
またその固有値は、
そのものである。
またその固有値は、![]() (これは実数) である
(一般に実数
(これは実数) である
(一般に実数 ![]() を、
を、![]() 型の実行列とみなすとき、
型の実行列とみなすとき、
![]() が
が ![]() に対して成り立つので、
に対して成り立つので、
![]() は
は ![]() の固有値で、
の固有値で、![]() が固有ベクトルである。)。
が固有ベクトルである。)。
ゆえに、定理を ![]() の場合に限定すると、
「
の場合に限定すると、
「![]() ならば
ならば ![]() は漸近安定、
は漸近安定、![]() ならば
ならば ![]() は不安定」
ということになる。
は不安定」
ということになる。
定理が成り立つのを納得したい、という人に向けて:
![]() が
が ![]() で微分可能であるとは
で微分可能であるとは
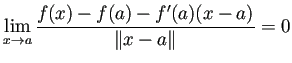
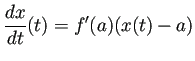
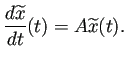 |
(G.2) |
これは定数係数線形常微分方程式と呼ばれる方程式である。 これについての “常識的事項” を知ると、 上の定理が感覚的に納得できると思われるので、 次項にまとめておく。