G..5 復習: 定数係数線形常微分方程式

$A\in \mathbb{R}^{n\times n}$ (つまり、は実数を成分とする次正方行列) とする。このとき

$\displaystyle \frac{\D x}{\D t}(t)=A x(t)$

(G.3)

について調べよう。この形の微分方程式は定数係数線形常微分方程式と呼ばれる。 (G.3) の解全体の集合を (G.3) の解空間と呼ぶ。 (G.3) の解空間は

次元線形空間の構造をもつ。その基底を(G.3) の解の基本系とか基本解と呼ぶ。

初期条件

$\displaystyle x(0)=x_0$

(G.4)

を満たす解は一意的に存在して、それは

$\displaystyle x(t)=e^{tA}x_0$

である。ここで

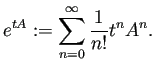
$\displaystyle e^{tA}:=\sum_{n=0}^\infty\frac{1}{n!}t^n A^n.$

(任意の複素数

に対して、この右辺の級数は収束する。)

$0\in\mathbb{R}^n$ は (G.3) の平衡点である。

$\begin{jtheorem}[$e^{tA}\to 0$の条件] $A\in \mathbb{C}^{n\times n}$\ に対�... ...� $\lambda$\ は $\MyRe\lambda<0$\ を満たす。 \end{enumerate}\end{jtheorem}$

$\begin{jcorollary}% latex2html id marker 3593 [$\max\MyRe\lambda<0$\ ならば $... ...形常微分方程式}) の漸近安定な平衡点である。 \end{jcorollary}$

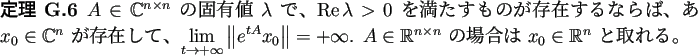
$\begin{jtheorem} $A\in \mathbb{C}^{n\times n}$\ の固有値 $\lambda$\ で、 ... ...^{n\times n}$\ の場合は $x_0\in\mathbb{R}^n$\ と取れる。 \end{jtheorem}$

$\begin{jcorollary}% latex2html id marker 3607 [$\max\MyRe\lambda>0$\ ならば $... ...線形常微分方程式}) の不安定な平衡点である。 \end{jcorollary}$

証明には、の Jordan標準形を用いるのが簡単である。行列のJordan標準形は、線形代数の話題であるが、時間や紙数の事情から省略されたり、はしょった説明を強行されたりすることが多い。くわしい (計算例も多くて参考になる) 本として、杉浦・横沼 [42] を紹介しておく。この本は定数係数線形常微分方程式にも詳しい。

証明のメインの部分だけならば、桂田 [43] で読むことができる。

一般に、安定であるが、漸近安定ではない平衡点のことを中立安定な平衡点と呼ぶことがある。 (G.3) について、 0 が中立安定であるための必要十分条件も知られているが (桂田 [43] に書いておいた)、線形安定性解析には役立たないので (平衡点が、線形化した微分方程式で中立安定であっても、もとの微分方程式で不安定となることがありうる)、ここでは省略する。

桂田祐史