Next: 3.3 解の漸近挙動, 平衡点とその安定性 Up: 3 logistic 方程式 Previous: 3.1 Malthusのモデルの修正としての logistic 方程式
(C.22) に加えて、初期条件
| (3.3) |
しばらく (とりあえず) ![]() は実数の定数としておく
(人口の場合、負の数はナンセンスであるが)。
は実数の定数としておく
(人口の場合、負の数はナンセンスであるが)。
| 細かい話 (解の存在範囲) -- 最初はスルーしても良いです |
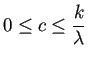 の場合、
(G.3) の分母は 0 にならないが、
そうでない場合は、
分母は の場合、
(G.3) の分母は 0 にならないが、
そうでない場合は、
分母は
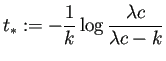 のとき
(のみ) 0 になる。 のとき
(のみ) 0 になる。
|