- ... の消去法を工夫したものとみなせる1
- LU分解
そのものは Gauss の消去法と無関係に定義され、
Gauss の消去法以外の方法で計算することも可能である。
Gauss の消去法は LU 分解を求めるための代表的なアルゴリズムである、
というに過ぎない。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
(証明を省略して2
- 大部分は簡単であるから、
自分で証明を試みるとよい。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 逆行列は下三角行列である3
- 証明は、
例えば桂田 [4] の第4章 (2009年9月24日現在) に書いてある。
一つの証明のアウトラインを書いておく:
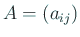 ,
,
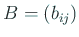 を共に下三角行列で、
を共に下三角行列で、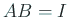 ,
,
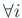
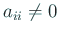 が成り立つとすると、
が成り立つとすると、
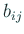 が簡単に求められる。
なお、後の余談 2.1 も見よ。
が簡単に求められる。
なお、後の余談 2.1 も見よ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... のすべての主座小行列式4
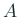 の
の 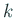 次の主座小行列
(首座小行列とも呼ぶ) とは、
次の主座小行列
(首座小行列とも呼ぶ) とは、
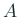 の最初の
の最初の 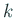 行
行 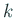 列から得られる
列から得られる 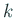 次の正方行列のことをいう。
その行列式のことを
次の正方行列のことをいう。
その行列式のことを 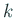 次の主座行列式と呼ぶ。
次の主座行列式と呼ぶ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
適当な置換行列5
- 知らないという人がいたので、
簡単に説明しておく。
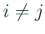 のとき、
のとき、
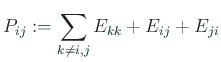 とおくと、
とおくと、
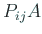 は
は 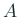 の第
の第 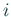 行と第
行と第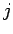 行が入れ替えた行列となる。
いくつかの
行が入れ替えた行列となる。
いくつかの 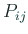 の積として得られる行列
の積として得られる行列 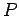 を置換行列という。
を置換行列という。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 回の乗除算で十分である6
- 計算にどれくらい手間がかかるかを計るために、
基本的な演算の回数を数えるという方法がある。
しばしば、
四則演算のそれぞれについて数える代りに、
乗除算の回数だけを数えて目安にする、という手段が採用される
(4次元ベクトルよりは1つの数値が分かりやすい)。
もう少し詳しいことが知りたければ、
例えば桂田 [4] を見よ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
けることになる7
- 細かい話をすると、
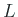 が単位下三角行列である場合は、
割り算の回数が
が単位下三角行列である場合は、
割り算の回数が 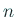 回減って、
回減って、
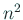 回の乗除算で解けることになる。
逆行列を知っている場合、
連立1次方程式は
回の乗除算で解けることになる。
逆行列を知っている場合、
連立1次方程式は 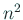 回の掛け算で解けるが、
それと互角であることが分かる。
回の掛け算で解けるが、
それと互角であることが分かる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
これは計算で示すことも出来るし8
-
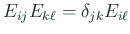 という公式が成り立つことに注意すれば、
という公式が成り立つことに注意すれば、
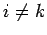 であれば
であれば
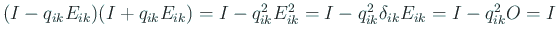 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... まだ説明していない概念9
- 例えば、
桂田 [4] などを見よ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...実対称行列の符号10
- 符号の定義とか、
Sylvester の慣性律とか、線形代数で習うべきことだと思うが、
残念ながら授業では省略されることもあるようである。
定番の齋藤 [5], 佐武 [7] などを見よ。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...これから容易に11
- 念のため書いておくと、
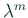 が 0 に収束するために
が 0 に収束するために
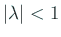 が必要で、
逆にこのとき任意の
が必要で、
逆にこのとき任意の 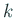 に対して
に対して
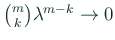 (
(
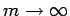 )
が分かるので、
)
が分かるので、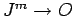 となるための十分条件である。
となるための十分条件である。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...この命題の証明を直接行うことも出来るが12
-
さわりの部分は
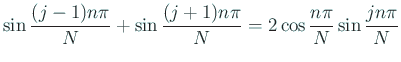 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
さらに、もしこの仮定が成り立たない、すなわち13
- ド・モルガン則など、
論理の法則を使って計算すると、機械的に計算できる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
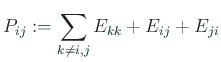 とおくと、
とおくと、
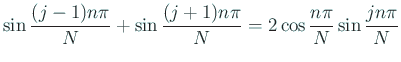 .
.