Next: 3.3 гҒ®гӮ№гғҡгӮҜгғҲгғ«и§Јжһҗ Up: 3 иЎҢеҲ—жі•гҒ«гӮҲгӮӢе®үе®ҡжҖ§и§Јжһҗ Previous: 3.1 е·®еҲҶи§ЈгҒҜгҖҢзӯүжҜ”гғҷгӮҜгғҲгғ«еҲ—гҖҚ
(иЎҢеҲ—гҒ®еҲ—гӮ’гҖҢиЎҢеҲ—еҲ—гҖҚгҒЁгҒ„гҒҶгҒ®гҒҜдҪ•гҒӢж°—гҒҢеј•гҒ‘гӮӢгҒ®гҒ§гҖҒ гғһгғҲгғӘгғғгӮҜгӮ№еҲ—гҒЁгҒ„гҒҶгҒ“гҒЁгҒ«гҒҷгӮӢгҖӮ)
![\begin{jproposition}[зӯүжҜ”ж•°еҲ—иЎҢеҲ—зүҲгҒ®и§Јжһҗ]
$A\in M(n;\C)$ гҒЁгҒ—гҒҰг...
...ҸеӨҡй …ејҸгҒ®еҚҳж №гҒ§гҒӮгӮӢгҖӮ
\end{enumerate}\end{enumerate}\end{jproposition}](img209.gif)
|
 | |||

д»»ж„ҸгҒ®иҮӘ然数 ![]() гҒ«еҜҫгҒ—гҒҰ
гҒ«еҜҫгҒ—гҒҰ
![]() гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
гҒ§гҒӮгӮӢгҒӢгӮүгҖҒ
![]() гҒ«й–ўгҒҷгӮӢж•°еӯҰзҡ„её°зҙҚжі•гҒ«гӮҲгӮҠгҖҒе®№жҳ“гҒ«
гҒ«й–ўгҒҷгӮӢж•°еӯҰзҡ„её°зҙҚжі•гҒ«гӮҲгӮҠгҖҒе®№жҳ“гҒ«
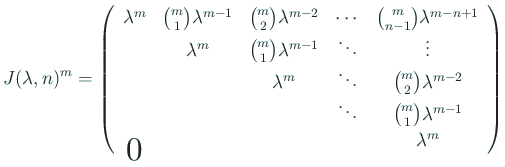
гҒ“гӮҢгҒӢгӮүе®№жҳ“гҒ«11
дёҖж–№гҖҒжҳҺгӮүгҒӢгҒ«
![]() гҒ®е ҙеҗҲгӮ’иҖғгҒҲгӮҲгҒҶгҖӮ
гҒ®е ҙеҗҲгӮ’иҖғгҒҲгӮҲгҒҶгҖӮ
![]() гҒ®еҜҫи§’жҲҗеҲҶ
гҒ®еҜҫи§’жҲҗеҲҶ ![]() гҒҜжңүз•ҢгҒ§гҒӮгӮӢгҖӮ
гҒҜжңүз•ҢгҒ§гҒӮгӮӢгҖӮ
![]() гҒқгҒ®гӮӮгҒ®гҒҢжңүз•ҢгҒ§гҒӮгӮӢгҒҹгӮҒгҒ«гҒҜгҖҒ
гҒқгҒ®гӮӮгҒ®гҒҢжңүз•ҢгҒ§гҒӮгӮӢгҒҹгӮҒгҒ«гҒҜгҖҒ![]() гҒҢеҝ…иҰҒеҚҒеҲҶгҒ§гҒӮгӮӢгҖӮ
гҒҢеҝ…иҰҒеҚҒеҲҶгҒ§гҒӮгӮӢгҖӮ
гҒҫгҒҹ
![]() гҒ®гҒЁгҒҚ
гҒ®гҒЁгҒҚ
![]() гҒҢеҸҺжқҹгҒҷгӮӢгҒҹгӮҒгҒ«гҒҜгҖҒ
гҒҫгҒҡеҜҫи§’жҲҗеҲҶ
гҒҢеҸҺжқҹгҒҷгӮӢгҒҹгӮҒгҒ«гҒҜгҖҒ
гҒҫгҒҡеҜҫи§’жҲҗеҲҶ ![]() гҒҢеҸҺжқҹгҒҷгӮӢеҝ…иҰҒгҒҢгҒӮгӮӢгҖӮ
гҒқгҒ®гҒҹгӮҒгҒ®жқЎд»¶гҒҜ
гҒҢеҸҺжқҹгҒҷгӮӢеҝ…иҰҒгҒҢгҒӮгӮӢгҖӮ
гҒқгҒ®гҒҹгӮҒгҒ®жқЎд»¶гҒҜ ![]() .
гҒқгҒ—гҒҰ
.
гҒқгҒ—гҒҰ
![]() гҒҜжңүз•ҢгҒ§гҒӘгҒ‘гӮҢгҒ°гҒӘгӮүгҒӘгҒ„гҒӢгӮүгҖҒ
дёҠгҒ«иҝ°гҒ№гҒҹгӮҲгҒҶгҒ«
гҒҜжңүз•ҢгҒ§гҒӘгҒ‘гӮҢгҒ°гҒӘгӮүгҒӘгҒ„гҒӢгӮүгҖҒ
дёҠгҒ«иҝ°гҒ№гҒҹгӮҲгҒҶгҒ« ![]() гҒҢеҝ…иҰҒгҒ§гҒӮгӮӢгҖӮ
йҖҶгҒ«
гҒҢеҝ…иҰҒгҒ§гҒӮгӮӢгҖӮ
йҖҶгҒ« ![]() гҒӢгҒӨ
гҒӢгҒӨ ![]() гҒ§гҒӮгӮӢгҒЁгҒҚгҖҒ
гҒ§гҒӮгӮӢгҒЁгҒҚгҖҒ
жңҖе°ҸеӨҡй …ејҸгҒ®еҚҳж №гҒ§гҒӮгӮӢгҒЁгҒҜгҖҒ
еҜҫеҝңгҒҷгӮӢ Jordan зҙ°иғһгҒ®гӮөгӮӨгӮәгҒҢ ![]() (гҒӨгҒҫгӮҠгҒҹгҒ гҒ®иӨҮзҙ ж•°) гҒ§гҒӮгӮӢгҒ“гҒЁгҒ«д»–гҒӘгӮүгҒӘгҒ„гҖӮ
(гҒӨгҒҫгӮҠгҒҹгҒ гҒ®иӨҮзҙ ж•°) гҒ§гҒӮгӮӢгҒ“гҒЁгҒ«д»–гҒӘгӮүгҒӘгҒ„гҖӮ
жЎӮз”° зҘҗеҸІ