2.6.2 実対称行列の正値性・負値性の判定、符号

(どうも「符号を授業で習っていない」ことが少なくないようで、困ったものである。正値性・負値性の判定は重要であるから、それだけ切り離して読めるようにすべきかもしれない。)

実対称行列の符号¹⁰(正の固有値の個数と負の固有値の個数の組) を求めるにも、LU 分解はしばしば有効である。

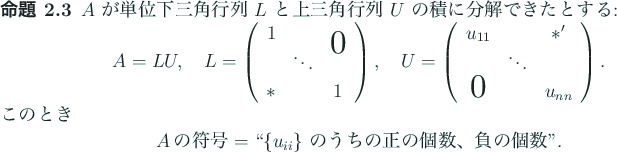
$\begin{jproposition} $A$ が単位下三角行列 $L$ と上三角行列 $U$\... ... のうちの正の個数、負の個数''}. \end{displaymath}\end{jproposition}$

証明. $(L^{-1})^T=:{\cal U}$ とおくと、

$\displaystyle {\cal U}^T A{\cal U}=U{\cal U}$

であるから、

の符号は $U{\cal U}$ の符号と等しい。ところが、

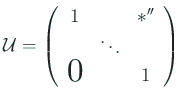
$\displaystyle {\cal U}= \left( \begin{array}{ccc} 1 & & *''\\ & \ddots & \\ \bigzerol & & 1 \end{array} \right)$

であるから、

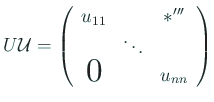
$\displaystyle U{\cal U} = \left( \begin{array}{ccc} u_{11} & & *'''\\ & \ddots & \\ \bigzerol & & u_{nn} \end{array} \right)$

であり、この行列の符号は $\{u_{ii}\}$ のうちの正であるものの個数、負であるものの個数の組に他ならない。 $\qedsymbol$ $\qedsymbol$

次項で見るように、実対称行列が正値であれば、 Gauss の消去法により、必ず LU 分解が可能である。従って、上に書いた変形は必ず可能である。つまり、与えられた実対称行列が正値であるかどうかを判定するには、 (ピボット選択無しの) Gauss の消去法の前進消去法が最後まで実行でき、その結果できる上三角行列の対角成分がすべて正であるかどうかを見れば良い。 (途中で対角成分が 0 になったり負になったりしたら、正値でないことが分かる)。行列が負値であることの判定も同様である。