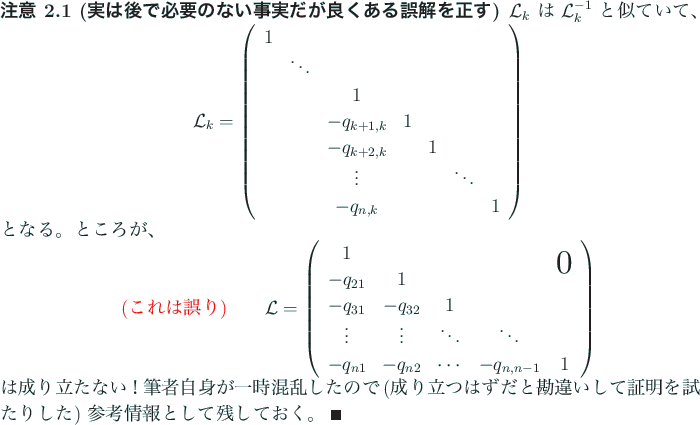
Next: 2.4.1 疎性が保存されるか Up: 2 LU分解 Previous: 2.3 LU分解を用いた連立1次方程式の解法
実は、Gauss の消去法は LU 分解を計算していることに相当する。 このことを理解すれば、LU 分解の計算法を知っていることになる。 Gauss の消去法が最後まで実行できるためには、 消去の過程で現れる対角成分が 0 にならないことが必要十分であるが、 この項では、それが常に満たされるとして議論する (その条件を吟味することは後の 2.7 で行う)。
Gauss の消去法では、 「行に関する基本変形」で係数行列を上三角行列に変形したが、 「行に関する基本変形」は基本行列を左からかけることに相当する (このことは基本変形を説明してある線形代数の教科書ならば、 必ず解説してあるはずであるが、 桂田 [4] の第4章にも書いておいた)。
![]() 次正方行列
次正方行列
![]() の
の ![]() 成分
成分 ![]() で
で ![]() 成分 (
成分 (![]() ) を掃き出すには、
第
) を掃き出すには、
第 ![]() 行から、
第
行から、
第 ![]() 行の
行の
![]() 倍を引く、という操作をするわけだが、
これは
倍を引く、という操作をするわけだが、
これは
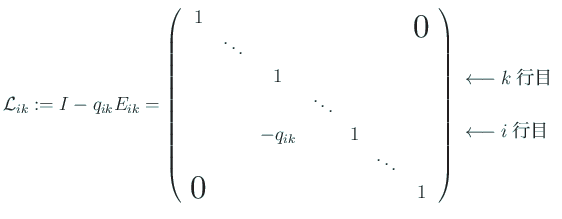
後で逆行列が必要になるので調べておこう。 まず

次に
上の操作
(
![]() を左からかける) を
を左からかける) を
![]() の順に行うと、
の順に行うと、
![]() の対角線よりも下の部分は掃き出されて、上三角行列になる:
の対角線よりも下の部分は掃き出されて、上三角行列になる:
各
![]() が単位下三角行列であるから、
が単位下三角行列であるから、![]() も単位下三角行列である。
ゆえに
も単位下三角行列である。
ゆえに ![]() は正則で、
逆行列
は正則で、
逆行列
![]() (
(
![]() ) も単位下三角行列である。
ゆえに (2) に左から
) も単位下三角行列である。
ゆえに (2) に左から ![]() をかけると、
をかけると、
実はより具体的に
(3) (1) の証明と同様に基本変形の意味を考えても分かるが、 ここでは地道な計算で示してみよう。
各 ![]() に対して
に対して
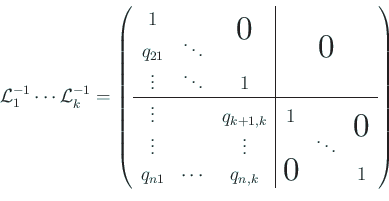
![]() のとき成り立つことは明らかである
(式 (1) から、
のとき成り立つことは明らかである
(式 (1) から、
![]() がこの形をしていることがすぐ分かる)。
がこの形をしていることがすぐ分かる)。
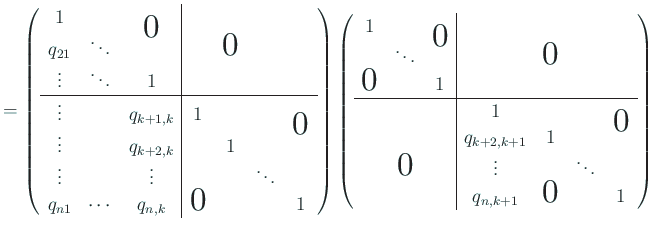
次に ![]() のとき成立すると仮定する。
のとき成立すると仮定する。
 | ||
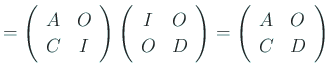 | ||
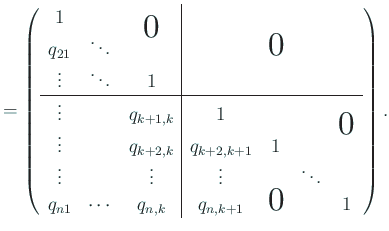 |