2.2.2 三角行列の性質

概観を得るために基本的な性質を証明抜きに述べておく (難しくはないから自力で証明にチャレンジしてもよい)。

下三角行列について得られる結果と並行した結果が上三角行列について得られるが、 以下では省略する (下三角行列についてのみ説明する)。

$n$次下三角行列 $L=(\ell_{ij})$について、

$$\det L=\prod_{i=1}^n \ell_{ii}.$$

すなわち、下三角行列の行列式は、すべての対角成分の積である。 ゆえに、下三角行列が正則であるためには、 すべての対角成分が 0 でないことが必要十分である。 特に単位下三角行列は正則である。

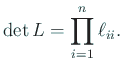
下三角行列同士の 和、差、積、 また (存在する場合の) 逆行列は下三角行列である³。

正則な下三角行列全体は乗算に関して群をなす。 特に単位下三角行列全体はその部分群となる。