3 ESIRモデル (で線形安定性解析を体験する)

(文献をチェックしておくこと。)

SIRモデルでは、最終的には感染者人口が0になる (感染症が終息する)。 それは感受性人口の補充がないからであると考えられる。

SIRモデルの仮定を修正し、 出生と自然死 (その感染症以外の理由での死亡) があると仮定した エンデミックス SIR モデル (ESIRモデル) を紹介し、 平衡点の線形化安定性解析をしてみよう。

ここで使う定理は1つだけ、ということも出来るが、 定数係数線形常微分方程式 ( 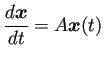$\dfrac{\D\bm{x}}{\D t}=A\bm{x}(t)$, 2次元ならば 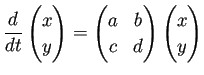$\dfrac{\D}{\D t} \begin{pmatrix}x y \end{pmatrix}=\begin{pmatrix}a & b c & d \end{pmatrix} \begin{pmatrix}x y \end{pmatrix}$ という形) の解について学んでおいた方が良い。 これについては、 数値シミュレーションして “遊ぶ” 経験をしておくのがお勧めである。