Next: 3.3 の安定性を調べる Up: 3 ESIRモデル (で線形安定性解析を体験する) Previous: 3.1.0.1 問
![$\displaystyle f(S,I)=\bm{0}
\quad\Iff\quad
\left\{
\begin{array}[ht]{ll}
b-S(\mu+\beta I)=0\\
I(\beta S-(\mu+\gamma))=0
\end{array} \right.
$](img85.png)
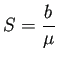 .
ゆえに
.
ゆえに
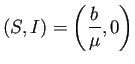 .
.
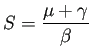 .
.
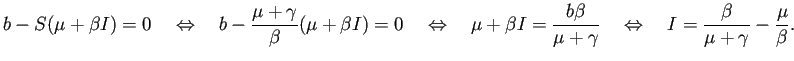
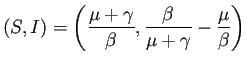 .
.
簡単のため
| (8) | 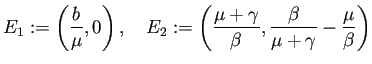 |
![]() は感染者が存在する平衡状態 (平衡点) である。
SIRモデルの場合には、そのような平衡点は存在しなかった
(感染者数が0でない限り、感受性者数は狭義単調減少)。
出生による感受性者の増加(供給)と、
感染と自然死による “減少” がつり合うことで、
平衡状態になっている。
は感染者が存在する平衡状態 (平衡点) である。
SIRモデルの場合には、そのような平衡点は存在しなかった
(感染者数が0でない限り、感受性者数は狭義単調減少)。
出生による感受性者の増加(供給)と、
感染と自然死による “減少” がつり合うことで、
平衡状態になっている。
![]() は感染者が存在しない状態である。SIR モデルと似ているが、
SIRモデルの場合は、
は感染者が存在しない状態である。SIR モデルと似ているが、
SIRモデルの場合は、![]() 軸上の任意の点
軸上の任意の点 ![]() が平衡点であったが、
ここではただ一つの点
が平衡点であったが、
ここではただ一つの点
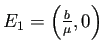 である。
(
である。
(
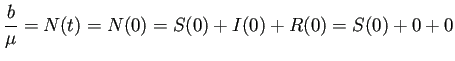 であるから
であるから
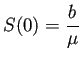 .)
.)