Next: 3.2 平衡点は2つある Up: 3.1 出生と自然死を考慮する ESIRモデル Previous: 3.1 出生と自然死を考慮する ESIRモデル
念のため注意: ![]() としてあるので、
としてあるので、
![]() である。
である。
以下では簡単のため、
この条件
(7)
が満たされる場合のみ考える。
このとき ![]() が定数であるから、
が定数であるから、![]() と
と ![]() が分かれば
が分かれば ![]() が求まる。
が求まる。
![]() と
と ![]() を定めるには、
(5a), (5b) のみあれば良い。
を定めるには、
(5a), (5b) のみあれば良い。
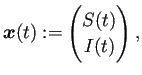
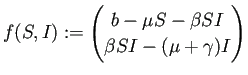
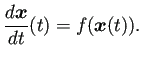
![]() のJacobi行列を求めておく。
のJacobi行列を求めておく。