3.1 出生と自然死を考慮する ESIRモデル

単位時間あたり $b$ 人誕生すると仮定する。 生まれた直後は感染していない、すなわち感受性者であるとする (現実の感染症では、母親から感染するという場合もあるらしいが)。

また、感受性者も、感染者も、回復者も、 単位時間当たり一定の割合 $\gamma$ (単位は、人/単位時間) で (その感染症でない理由によって) 死亡すると仮定する。感染症が理由でないことを表すため「自然死」と呼ぶ。

次の方程式を満たすと考えるのが自然であろう。

初期値 $S(0)$, $I(0)$, $R(0)$ については、これまでと同様に以下を仮定する。

$$S(0)>0,\quad I(0)\ge 0,\quad R(0)=0.$$ (6)

$N(t):=S(t)+I(t)+R(t)$ とおくと、

$$\frac{\D N}{\D t}(t)=b-\mu(S(t)+I(t)+R(t))=b-\mu N(t).$$

$$N(0)=\frac{b}{\mu}$$ (7)

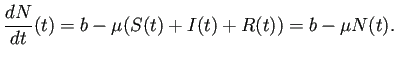
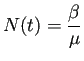ならば、任意の $t$ について $N(t)=\dfrac{\beta}{\mu}$ (定数) が成り立つ。