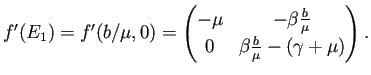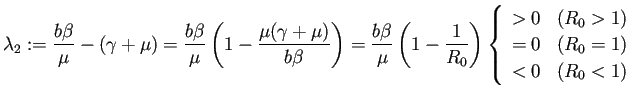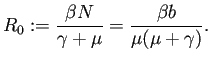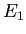 における
における 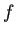 の Jacobi行列は
の Jacobi行列は
この行列の固有値は (対角成分であるから)
ただし 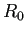 は、この場合の基本再生算数である:
は、この場合の基本再生算数である:
|
(9) |
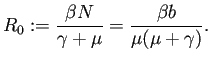 |
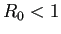 のとき、
のとき、
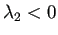 であるから、
であるから、
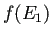 のすべて(2つ)の固有値の実部は負である。
ゆえに
のすべて(2つ)の固有値の実部は負である。
ゆえに 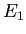 は漸近安定な平衡点である。
は漸近安定な平衡点である。
つまり、
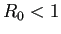 ならば感染者数
ならば感染者数 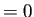 という状態
という状態 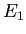 は、
漸近安定 (十分小さい任意の摂動は 0 に減衰する) である。
ちょっと感染者が出ても終息する、ということになる。
は、
漸近安定 (十分小さい任意の摂動は 0 に減衰する) である。
ちょっと感染者が出ても終息する、ということになる。
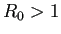 のとき、
のとき、
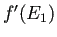 は正の固有値
は正の固有値 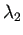 を持つので、
を持つので、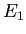 は不安定な平衡点である。
は不安定な平衡点である。
桂田 祐史
![]() における
における ![]() の Jacobi行列は
の Jacobi行列は