Next: 3 ESIRモデル (で線形安定性解析を体験する) Up: 2 SIR モデル Previous: 2.2 今後の見通し
(3a), (3b) は非線形方程式ということもあって、 解を解析的に求めることは(おそらく)出来ないが、 解軌道の方程式を求めることは出来る。 この辺は有名な Lotka-Volterraロトカ・ヴォルテラ の方程式 1や、Kepler運動2と事情が似ている。
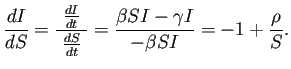
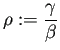
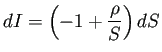
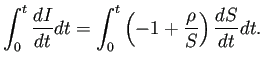
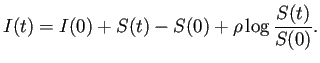
![]() ,
, ![]() ,
, ![]() ,
, ![]() をそれぞれ
をそれぞれ
![]() ,
, ![]() ,
, ![]() ,
, ![]() と書くと
と書くと
| (4) | 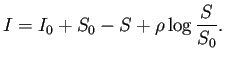 |
![]() ,
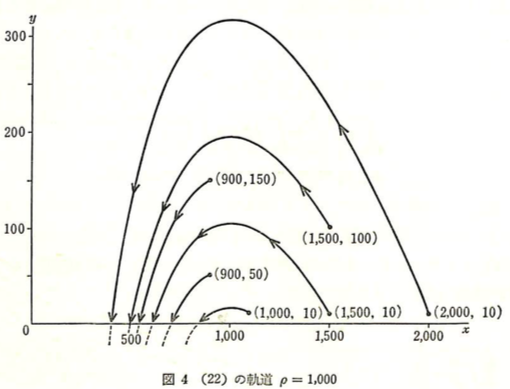
, ![]() を与えて、この曲線を描くのはコンピューターを使えば簡単である。
を与えて、この曲線を描くのはコンピューターを使えば簡単である。
![]() は
は ![]() の関数とみなすとき、
の関数とみなすとき、
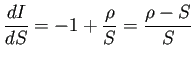
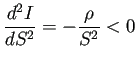
![]() や
や
![]() のとき
のとき
![]() .
.
(力学系は、![]() 軸上の点
軸上の点 ![]() を平衡点としていて、
任意の解について
を平衡点としていて、
任意の解について
![]() が成り立つ、それと矛盾はしないが、
混乱しないように注意が必要である。)
が成り立つ、それと矛盾はしないが、
混乱しないように注意が必要である。)
 |
初期時点
![]() を出発する点
を出発する点
![]() は、
時間がたつにつれて、この軌道の上を右から左に動いてゆく。そのわけは
は、
時間がたつにつれて、この軌道の上を右から左に動いてゆく。そのわけは
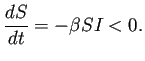
(ゼミ中に細かいところまで調べたような記憶があるが、 記録が残っていないのは残念なことだ…以下は記憶を手繰って)
例えば、
![]() を通る曲線と
を通る曲線と ![]() 軸との交点
軸との交点
![]() を求めるには、
を求めるには、
![]() についての方程式
についての方程式
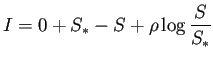
findS[S_, I_, rho_] :=
Module[{S0},
S0 /. FindRoot[I == 0 + S0 - S + rho Log[S/S0], {S0, rho/2}]]
S0=findS[2000, 10, 1000]
|
このようにして、
佐藤[8] p. 176の図4を再現してみた
(図2. やってみて気付いたが、
![]() という座標は
という座標は ![]() の誤植であろう)。
の誤植であろう)。
桂田 祐史