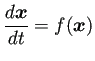Next: 2.3 解軌道 Up: 2 SIR モデル Previous: 2.1 SIRモデルの紹介
関係 (17) があるので、
![]() ,
, ![]() ,
, ![]() のうちの2つだけを考えれば十分である。
ここでは
のうちの2つだけを考えれば十分である。
ここでは ![]() と
と![]() を考えることにする。
を考えることにする。
この微分方程式は非線形であることもあり、 式変形で解を求めることはできない (と思われる。証明出来るかは知らないが。)。
しかし、任意の初期値
![]() に対して、
初期値問題の解
に対して、
初期値問題の解
![]() が一意的に存在することは、
常微分方程式の初期値問題の解の一意存在定理から容易に分かる。
が一意的に存在することは、
常微分方程式の初期値問題の解の一意存在定理から容易に分かる。
解
![]() は式変形で求められないが、実は解軌道の方程式は簡単に得られ、
それにより解の性質が色々分かる:
は式変形で求められないが、実は解軌道の方程式は簡単に得られ、
それにより解の性質が色々分かる:
![]() であれば、
であれば、
![]() は第1象限に止まり、
は第1象限に止まり、
![]() は単調減少し、ある正数
は単調減少し、ある正数 ![]() ,
,
![]() が存在して
が存在して
微分方程式 (3a), (3b) の右辺には ![]() が陽には現れない、すなわち
が陽には現れない、すなわち