Next: E..2 Euler法のプログラム例 (1次元) Up: E. 常微分方程式の数値計算入門 Previous: E. 常微分方程式の数値計算入門
未知関数
![]() についての1階正規形の常微分方程式
についての1階正規形の常微分方程式
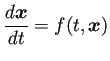 (
(
正規形というのは、方程式に現れる最高階の導関数 (1階なので
![]() ) について解かれている (つまり
) について解かれている (つまり
![]() 何とか という形で、右辺には
何とか という形で、右辺には
![]() は現れない)
ということを意味する。
は現れない)
ということを意味する。
2階以上の方程式は、簡単に1階の微分方程式に変換できるので、 (17) は、応用上十分に一般的な設定であろう。
初期条件としては
| (14) |
| (15) |
しばしば区間 ![]() を
を ![]() 等分する。この場合は
等分する。この場合は ![]() がすべて
がすべて
| (16) | 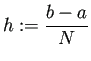 |
| (17) |
精度を確保するために、![]() を適当に選ぶことがある(刻み幅の自動調節)。
を適当に選ぶことがある(刻み幅の自動調節)。
![]() から
から
![]() を近似的に求めるために色々なやり方がある。
(注: ここから後の
を近似的に求めるために色々なやり方がある。
(注: ここから後の ![]() は、厳密には
は、厳密には
![]() と異なるので、
本当は別の記号を用いるべきかもしれない。)
と異なるので、
本当は別の記号を用いるべきかもしれない。)
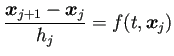 (
(
| (18) |
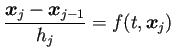 (
(
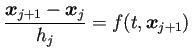 (
(
| (19) |
| (20) | 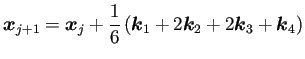 | |
| (21) | ||
| (22) | ||
| (23) | ||
| (24) |
本当は、
![]() ,
, ![]() ,
, ![]() ,
, ![]() は、
は、
![]() に依存するので、
例えば
に依存するので、
例えば
![]() ,
,
![]() ,
,
![]() ,
,
![]() のように
書くべきであろうが、多くの本でサボってある。
のように
書くべきであろうが、多くの本でサボってある。
桂田 祐史