2.1 SIRモデルの紹介

感染症の数理をじっくり勉強しようという人には、 有名なSIRモデルについてのていねいな説明が載っている 佐藤 [8] から読み始めるのがお勧めである。

この節では [8] に従って、SIRモデルの紹介をする。

言葉の説明から始める。

感染症

英語では infectious disease.

感受性者

(まだ感染していないので) これから感染する可能性がある人のこと。 英語では susceptible (individuals) というので、 感受性者の数 (the number of susceptible individuals, the stock of susceptible population) のことを文字 $S$ で表すことが多い。 巷では「感染予備軍」と訳す人もいるが正式な言葉かは不明。

感染者

英語では infectious individuals あるいは infected individuals というので、 感染者の数 (the number of infectious individuals, the stock of infected population) のことを文字 $I$ で表すことが多い。

回復者

感染してから治った人のことを回復者と呼ぶ。 免疫を獲得したのでもう感染することはないので、 感受性者と区別する。英語では recovered individuals というので、 回復者の数のことを文字 $R$ で表すことが多い。

感染症にかかると回復せずに死亡する場合もあるし、 回復する前に発見されて隔離される場合もある。 回復者、死亡者、隔離者をまとめて除去者と呼び、 その数を $R$ と表す、とする立場もある。

空間分布を考えず、人数の時間変化を考えることにして、 時刻 $t$ における感受性者、感染者、回復者の数を $S(t)$, $I(t)$, $R(t)$ で表すことにする。

適当な仮定をおくと、次の連立微分方程式が導かれる。

ここで $\beta$, $\gamma$ は正定数である。

(1a), (1b), (1c) を SIR モデルと呼ぶ。

これは、 1927年に出版された William Ogilvy Kermack と Anderson Gray McKendrick の論文 [9] で提案されたので、 Kermack-McKendrick モデルとも呼ばれている。

ちなみに [9] では、 $S(t)$, $I(t)$, $R(t)$ をそれぞれ $x_t$, $y_t$, $z_t$ で表し、 “the number of individuals still unaffected”, “the total number who are ill”, “the number who have beeen removed by recovery and death” と説明している。

すぐ分かるように SIR モデルでは総人口が一定である (死亡することを考えない、あるいは死者も数えるから、当たり前)。

証明. 任意の $t$ に対して、

$$N'(t) =S'(t)+I'(t)+R'(t) =-\beta S(t)I(t)+\left(\beta S(t)I(t)-\gamma I(t)\right)+\gamma I(t)=0$$

であるから、$N(t)$ は定数である。$\qedsymbol$ $\qedsymbol$

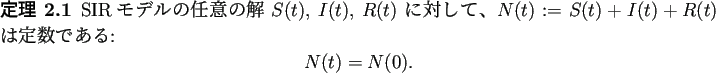
$N(0)$ を単に $N$ と表すと

$$S(t)+I(t)+R(t)=N.$$ (2)