5.4 解を求めて … まず局所解の存在と一意性

(理論的な話に慣れいてない人、特に初めて読む場合は、 軽く読み流すだけで良いです。 一方、この部分は実はほとんどいつでもワンパターンなので、 この機会に少し時間をかけて学ぶ価値は高いと思います。)

コンピューター・シミュレーションで相当のことが “分かる” けれども、 例えば周期解になるらしい、ということが分かっても、本当に周期解だろうか？ という疑問に答えるには、数学的な考察が必要になる。

ここでは、まず局所解が存在すること、 それがただ一つであること (解の一意性、単独性) をどのように確認するか考えよう。

(初期値問題の局所解とは: 解は関数であり、 変数のどういう範囲について定義されているかという定義域がある。 解の存在を保証する定理の多くは、 初期時刻 $t_0$ から十分短い時間の間は、 微分方程式を満たす関数が存在する、 という形をしている。 そのような定義域が狭い範囲に限定された(短い時間の間の)解のことを局所解と呼ぶ。)

微分方程式 (C.17) の右辺に現れる関数 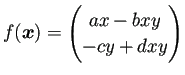$f(\bm{x})=\begin{pmatrix}ax-bxy \\ -cy+dxy \end{pmatrix}$ は、 各成分が多項式なので、$C^\infty$ 級の関数である。

特に$f$ は連続であるから、局所解が存在することが分かる (付録 D.2 の 定理D.1)。 長い時間が経っても解が存在するかどうかは、この段階ではまだ分かっていない (後述する)。

また $f$ は $C^1$級であるから、解の一意性が成り立つことが分かる (付録 G.3 の定理D.9)。 一意性と言われてもピンと来ないかもしれないが、後で意外と使うことになる。

(Malthusの法則や、logistic equation などのように、 微分方程式の解がこういう式で表される、ということが示せたとき、 解の公式が得られただけでなく、解の一意性も (多くの場合は) 同時に示せたことになる。 そのため、具体的な式で解ける問題ばかり調べていると、 一意性にあまり注意を払わずに済んでしまう (「そういうことをする必要はあるんですか？」)。 しかし、解を表す式が得られない場合は、解の一意性だけでも分かると、 色々と有効である。)