(F.5) の解空間の次元は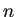 であることを証明することが
大事な目標であるが、
まず1次独立性(線形独立性)の定義を想い出そう。
であることを証明することが
大事な目標であるが、
まず1次独立性(線形独立性)の定義を想い出そう。
線形空間 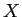 の要素
の要素 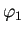 ,
,  ,
, 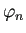 が1次独立であるとは
が1次独立であるとは
![$\displaystyle (\forall c_1,\cdots,c_n\in\mathbb{R})\quad \left[ c_1\varphi_1+\cdots+c_n \varphi_n=0\THEN c_1=\cdots=c_n=0 \right]$](img866.png) |
(F.6) |
が成り立つことをいう。
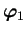 ,
,  ,
,
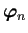 が
線形同次微分方程式
が
線形同次微分方程式
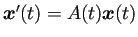 (
(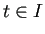 ) の解である場合は、
) の解である場合は、
は
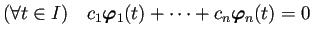 |
(F.7) |
を意味する。このことは容易に理解できるが、
この条件
(無限個の 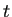 について等式が成り立つ)を確認するのは、
一見してそれほど簡単でないように思われるかもしれない。
実は、
この後紹介する定理 F.3 によると、
線形同次微分方程式
について等式が成り立つ)を確認するのは、
一見してそれほど簡単でないように思われるかもしれない。
実は、
この後紹介する定理 F.3 によると、
線形同次微分方程式
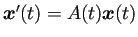 の
の
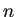 個の解
個の解
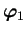 ,
, 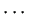 ,
,
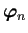 に対しては、
任意に選んだ1つの
に対しては、
任意に選んだ1つの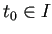 に対して
に対して
が成り立つことを確認すれば良い。
証明.
(
F.9) を証明しよう。
行列
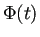
の第
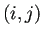
成分を
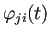
と表すことにする
(
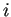
番目の解であるベクトル値関数
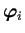
の第
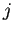
成分である
--
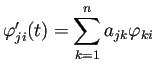
(
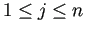
)
が成り立つことに注意する)。
(
F.9) を解けば
(
G.3) が得られる。


この定理から 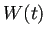 について、
について、
- (a)
- 任意の
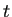 に対して
に対して 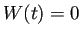 であるか
であるか
- (b)
- 任意の
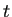 に対して
に対して 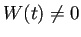 であるか
であるか
どちらか一方のみが成り立つが成り立つことが分かる。
ゆえに、ある 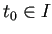 に対して、
に対して、
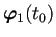 ,
, 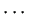 ,
,
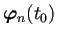 が
が
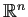 の1次独立なベクトルならば、
の1次独立なベクトルならば、
(a) が成り立たないので、(b) が成り立つ。すなわち任意の 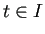 に対して
に対して
これは
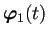 ,
,  ,
,
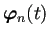 が
が
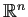 の1次独立なベクトルであることを意味する。
の1次独立なベクトルであることを意味する。
Subsections
桂田 祐史
![]() であることを証明することが
大事な目標であるが、
まず1次独立性(線形独立性)の定義を想い出そう。
であることを証明することが
大事な目標であるが、
まず1次独立性(線形独立性)の定義を想い出そう。
![]() の要素
の要素 ![]() ,
, ![]() ,
, ![]() が1次独立であるとは
が1次独立であるとは
![]() ,
, ![]() ,
,
![]() が
線形同次微分方程式
が
線形同次微分方程式
![]() (
(![]() ) の解である場合は、
) の解である場合は、
![\begin{jdefinition}[Wronskian]
$I$は $\mathbb{R}$の区間、$A\colon I\to\mat...
...ski} 行列式}あるいは %
\textbf{Wronskian} と呼ぶ。
\end{jdefinition}](img873.png)
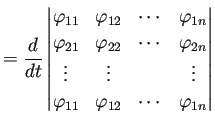
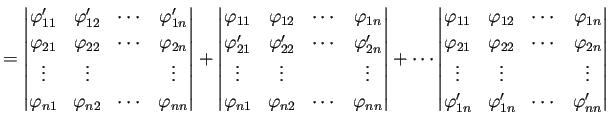
![\begin{jtheorem}[Wronskianの満たす微分方程式]
$I$は $\mathbb{R}$の�...
...nolimits A(s)\;\D s\right)
\quad\text{($t\in I$)}.
\end{equation}\end{jtheorem}](img874.png)
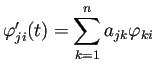 (
(
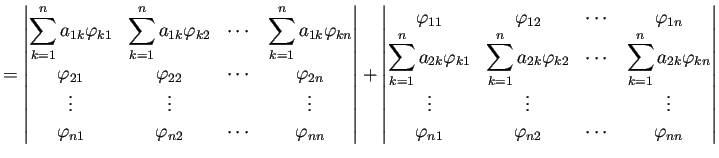
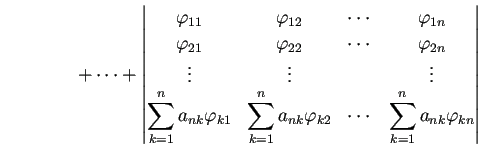
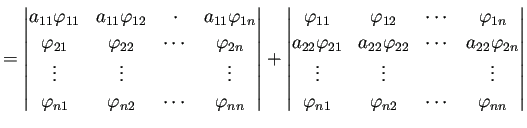
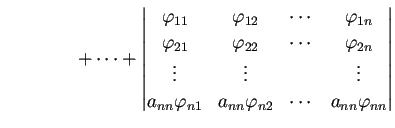
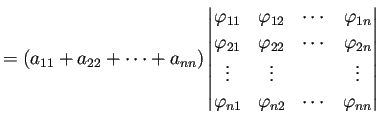
![]() について、
について、