F..5.1 ロンスキアンを用いない方法

(しばらく工事中)

ロンスキアンを用いた議論は分かりやすいが、ロンスキアンが登場しないテキストも結構ある。実は解の一意性定理だけで十分であるようだ。

定理を述べて証明する前に、二、三注意しておく。

$\varphi_1$ , $\cdots$ , $\varphi_n$ が1次独立という条件は

$\displaystyle c_1\varphi_1+\cdots+c_n\varphi_n=0\THEN c_1=\cdots=c_n=0$

の形で述べられることが多いが、以下では対偶

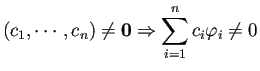
$\displaystyle (c_1,\cdots,c_n)\ne\bm{0}\THEN \sum_{i=1}^n c_i\varphi_i\ne 0$

の形で用いる。

関数として1次独立・1次従属という場合、と $\ne 0$ は定数関数0 に等しい、等しくないということであるから、

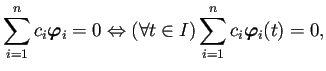
$\displaystyle \sum_{i=1}^nc_i\bm{\varphi}_i=0 \Iff (\forall t\in I) \sum_{i=1}^nc_i\bm{\varphi}_i(t)=0,$

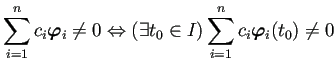
$\displaystyle \sum_{i=1}^nc_i\bm{\varphi}_i\ne 0 \Iff (\exists t_0\in I) \sum_{i=1}^nc_i\bm{\varphi}_i(t_0)\ne 0$

である。

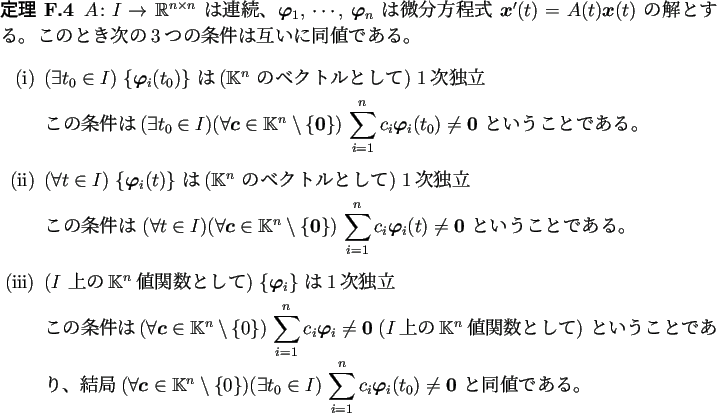
$\begin{jtheorem} $A\colon I\to\mathbb{R}^{n\times n}$\ は連続、 $\bm{\varph... ...bm{\varphi}_i(t_0)\ne\bm{0}$ と同値である。 \end{enumerate}\end{jtheorem}$

この定理の中の「1次独立」を「1次従属」に置き換えた次の命題が成立する (実際、次の命題の (i), (ii), (iii) の条件は、それぞれ上の定理の (ii), (i), (iii) の否定であるから、上の定理から、互いに同値である。)。

$\begin{jtheorem} $A\colon I\to\mathbb{R}^{n\times n}$\ は連続、 $\bm{\varph... ...c_i\bm{\varphi}_i(t)=\bm{0}$ と同値である。 \end{enumerate}\end{jtheorem}$

では定理F.4を証明しよう。

(ちなみに Wronskian についての等式が分かっていると、以下の証明の (i) $\THEN$ (ii) と (iii) $\THEN$ (ii) の証明で、解の一意性定理を使わないですむ。)

証明. $\qedsymbol$

Subsections

桂田祐史