... ページあれば良いが¹

歴史を紹介してある 資料に数表の規模 (長さ) が載っていないのは変だと思う。 ほかの数値から推算できるだろうということなのだろうが、 すぐ後に述べるように到底信じられないようなことが書いてあったりするし。 本文やその訳は載せているくせに数表は一部だけとかいうのも、 改めてほしいものである。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Mercator²

有名な地図学者の Gerardus Mercator (1512-1594) と混同しないように。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 球面三角法³

カジョリ [14] には、 『学生諸君は、球面直角三角形の解法で、「ネイピアの類同式」と 「環状要素のネイピア法則」というものを記憶しているであろう。』 と書いているが、現代の学生には球面三角法はちんぷんかんぷんであろう。 正直私もそうである。 空間図形の問題をベクトルの計算で解いてしまう時代に、 球面三角法に実用的な意味はほとんどないであろう (学生時代に天文計算の本を読んでいて、 「昔は球面三角法が使われていたが…」というくだりを読んだ覚えがある。 つまりもう天文計算でも球面三角法は現役を引退しているということである。)。 ただ次の二つのことを指摘しておきたい。 (i) 筆者の手持ちの百科事典で球面三角法を引くと、中にネーピアが出て来る。 (ii) 現在の学生向けの数学のカリキュラムでは「平面三角法」 しか出て来ないわけだが、 歴史的には平面三角法よりも球面三角法の方がはるかに重要であった。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 後にオックスフォード大学に移り幾何学のサヴィル教授⁴

ボイヤー の訳注によると、 「サヴィル教授職とは、オックスフォードの幾何学天文台の教授であっ たヘンリー・サヴィル卿が 1619 年に創設した講座で、 こんにちまですぐれた教授により受け継がれている。」

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... の計算棒⁵

当初は対数よりも Napier の計算棒の 方が有名だったそうである。 ガリレオも「比例コンパス」という計算道具を売って生計の足しにしていたそうで、 計算を簡単にする手段が望まれていた時代であったのだろうか。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 天文学者の寿命を2倍にした⁶

余談になるが、 現代の若い人にとって、 対数が計算の手間を大きく軽減するということはぴんと来ないかもしれない。 筆者は高校生のときに 地学教師の方針で対数表を使った計算法を叩き込まれたためもあって、 対数の便利さは肌で感じることができた。 ちょうどその頃から一般家庭に電卓が普及しつつあったため、 対数を便利に感じた最後の世代かもしれない。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... の円における⁷

当時 小数はまだ十分普及していないため、 小数をさけるように工夫してある。 Napier が利用できた最良の三角関数表は 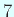$7$ 桁精度であったため、 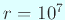$r=10^7$ という半径の円を考えたといわれている。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... の表を作成した⁸

非常に高精度であり、 また誤植が少ないということである。数表の作り方についても 詳しい説明が残されているので、 コンピューターで再現して付き合わせるということが可能と思う。 誰か挑戦しないかな… ちなみに http://www.ru.nl/w-en-s/gmfw/bronnen/napiertabellen.html で表の一部が読める。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 微分方程式解釈しても得られるし⁹

このやり方は、 結構あちこちで目にするが、個人的には、 ニュートン (Sir Isaac Newton, 1643-1727, 英国の Woolsthorpe に生まれ、 London にて没する) どころかガリレオ (Galileo Galilei, 1564-1642, イタリアの Pisa に生まれ Arcetri にて没する) 以前の人の数学を 微分方程式で説明するのは「少しやりすぎ」だと感じる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.