Next: A..0.0.1 注 Up: 対数の歴史 Previous: 5 気になっていること
E(君|さん)の卒研レポートのタイトルは「対数の世界」である。 本人の希望で一般公開はしないということで、 ここでは少し詳しく内容を紹介しておく。
ハイラー・ワナーには当然対数関数についても書いてあり、 普通対数の発見者とされる Napier についても一応は言及されているが、 常用対数の創始者とされる Briggs の計算法から本格的な議論を始めている。 残り時間が非常に限られていたのだが、 本人の強い希望で Napier について調べることになった。
Napier (1550-1617, Scotland の Edinburgh に生まれ、 Edingburgh にて没する) は、ガリレオ (Galileo Galiel, 1564-1642, Pisa に生まれ Arcetri にて没する) とほぼ同時代人で、 球面三角法や Napier の計算棒5(「Napier の骨」とも言う), 小数「点」を表すための記号として “.” を使うことの提唱などでも知られている。 対数を発見 (発明?) したのも球面三角法の計算の効率化 (それは「大航海時代」とも称される時代の要請でもあった) が動機であった。 200年程後になって、Laplace が
著書の序文によると対数について研究を始めたのは 1594 年頃で、
それから 20 年に渡って計算することで、
半径 ![]() の円における7、
0度から
の円における7、
0度から![]() 度までの
度までの![]() 分(
分(![]() 度) 刻みの角度
度) 刻みの角度 ![]() に対する正弦
に対する正弦
| Napierの対数の定義 |
|
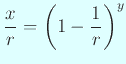
|
容易に
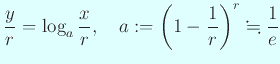
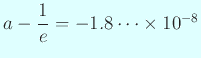 )。
)。
![]() の性質として、
の性質として、
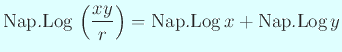
Napier のラテン語の論文 “Mirifici Logarithmorum Canonis Descriptio” が 1614 年に発表されると、 敏感に反応した人達がいた。 Edward Wright は 1616 年に英訳を発表している (http://www.ru.nl/w-en-s/gmfw/bronnen/napier1.html)。 また Henry Briggs は発表翌年 (1615年) の夏に、 馬で四日間の旅をして Napier を尋ねて一月ほど逗留し、 対数について議論したそうである。 常用対数の概念は二人の合作であるらしい。 Briggs は翌年の夏も Napier を尋ね、 さらにその翌年の夏も Napier を尋ねようとしていたが、 春に Napier がなくなって果せなかったという。
Napierの没後、 “Mirifici logarithmorum canonis constructio” が出版され、 対数表の作り方が公表された。 この論文の中で、小数点の