1.3 ビュルギ

Jobst Bürgi (1552-1632, スイスの...) は1603-1611の間に対数表を作り、 1620年に刊行した (“Tafeln arithmetischer und geometrischer Zahlenfolgen mit einer gründlichen Erläuterungen, wie sie zu verstehen sind und gebraucht werden können”)。

図 1: ”The Inventor of Logarithms” [] による

グレイゼル [9] によると、

• 有能な時計職人であったが、 ケプラー (Johannes Kepler, 1571-1630) の助手となり計算に従事した。
• シモン・ステヴィンの利率計算用の表が乗除算を加減算におきかえて簡単化する ために使えることにビュルギが気がつき、対数表の作成への刺激になった。
• ビュルギの仕事をケプラーは高く評価して公表するように再三勧めた (しかし公表しなかった)。
• 底として $a=1+10^{-4}$ を採用した。
• 次の1列目の数を「赤い数」、2列目の数を「黒い数」と呼んだ。
  $$\begin{array}{cccccccccc} \color{red}0,& \color{red}1, & \color{... ...r{red}4, & \color{red}5,\dots\\ 1, &a, &a^2,&a^3,&a^4,&a^5,\dots \end{array}$$

とのことである。

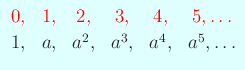
グレイゼルによると、ビュルギは $n$ を動かしたときの

$$10^8(1+10^{-4})^n$$

の表を与えていて、

$$10^8\left(1+10^{-4}\right)^{n^\ast}\kinji 10^9$$

となるまで計算している、それは「完全な赤い数 $23027002$」までであり、 2億回の計算をした、と書いてある。 しかしこれは何だかよく分からないぞ。

$$\left(1+10^{-4}\right)^{n^\ast}\kinji 10$$

を解くと

$$n^\ast\log_{10}\left(1+10^{-4}\right)=\log_{10}10=1$$

であるから

$$n^\ast=\frac{1}{\log_{10}\left(1+10^{-4}\right)}=23027.002203\cdots \kinji 23027.$$

はてさて何の間違いだろうか？

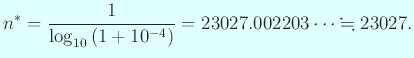
グレイゼル [9] の本に表の写しが載っていて、 それによると1ページに $50\times 8=400$ の数が載せられている (らしい)。 $n^\ast=23027$ 個の数値を載せるには、 単純計算で $58$ ページあれば良いが¹、 この $10^3$, $10^4$ 倍の規模の数表は考えにくい。変だなあ。

大体2億回の掛け算を7,8年でするとなると、1年に2500万回の掛け算。 1日に10万回近い掛け算。むちゃくちゃだな。 (私の結論: グレイゼルは何か勘違いをしている。) 全部で2万3000回ならば、4桁作業量は下がって 1 日 10 回程度だから、 まあ信じられる数値ではある。

ビュルギについて、 http://www.micheloud.com/FXM/LOG/index.htmで読んだことだが、 1588年には対数の考え方を手紙に書いているということである。 なお、このWWWページには対数表の1ページが載っている (ちょうどグレイゼルに載っているのと同じ部分だが、 1ページ全部見えているので情報量は多い)。

ちなみにカジョリ [14] には、

…この表は、

$$y=10^8(1.0001)^x$$

を与える。たとえば $10^8\cdot(1.0001)^{530}=100531380$

と書いてあるのだが、 $10^8(1.0001)^{530}=105442685.107\cdots$, $10^8(1.0001)^{53}=100531380.3455\cdots$ であるから、 カジョリも表の読み方が間違っている ($530$ 乗でなくて $53$ 乗だ)。