Next: H..1.1 離心近点距離 を平均近点距離 の関数として表す Up: H. Kepler の方程式とその解法 Previous: H. Kepler の方程式とその解法
2体問題では、Kepler の第1,第2法則によって、
惑星
![]() は、太陽
は、太陽
![]() を一つの焦点とする楕円軌道を描き、
任意の時刻に動径
を一つの焦点とする楕円軌道を描き、
任意の時刻に動径
![]() の掃く面積は、
その時間に比例する。
の掃く面積は、
その時間に比例する。
![]() の描く楕円を
の描く楕円を
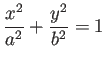
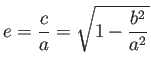
次のような「平均惑星」
![]() を考える
(これはここで作った用語で、「平均太陽」のもじりである)。
を考える
(これはここで作った用語で、「平均太陽」のもじりである)。
![]() が近日点を通る瞬間を時刻
が近日点を通る瞬間を時刻 ![]() とする。
また 点
とする。
また 点
![]() の、
の、
![]() を極とする極座標を
を極とする極座標を ![]() ,
, ![]() とする:
とする:
惑星
![]() の、
太陽
の、
太陽
![]() を極とする極座標の角度である
を極とする極座標の角度である ![]() は、
天文用語では、
近日点
は、
天文用語では、
近日点 ![]() から惑星までの角距離という意味で、
真近点距離 (true anomaly) と呼ばれる
5。
から惑星までの角距離という意味で、
真近点距離 (true anomaly) と呼ばれる
5。
離心近点距離 (eccentric anomaly) ![]() ,
平均近点距離 (mean anomaly)
,
平均近点距離 (mean anomaly) ![]() を
を
| Keplerの問題 |
|
|