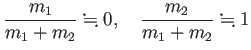Next: E. 平面運動であることの証明 Up: D. 太陽は動かないという仮定について Previous: D..3 太陽を座標系の原点とした方程式
![\begin{jproposition}[重心は等速直線運動する]
$\Vector{g}:=\dfrac{m_1...
...s.t.
$\Vector{g}=t\Vector{a}+\Vector{b}$ が導かれる。)
\end{jproposition}](img197.png)
|
![]() は、太陽と惑星からなる系の重心と呼ばれる。
(すぐ上で見たように) これが等速直線運動するので、
もともとの座標系が物理で言うところの慣性系である場合、
重心を中心とする座標系も慣性系になる。
前項の太陽を座標系の中心とするのよりは望ましいであろう。
は、太陽と惑星からなる系の重心と呼ばれる。
(すぐ上で見たように) これが等速直線運動するので、
もともとの座標系が物理で言うところの慣性系である場合、
重心を中心とする座標系も慣性系になる。
前項の太陽を座標系の中心とするのよりは望ましいであろう。
重心を原点とした場合の惑星の位置ベクトルは
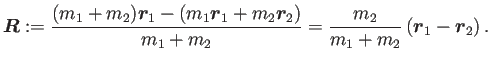
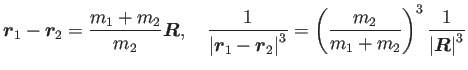
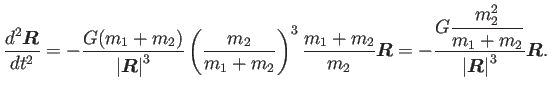
そこで
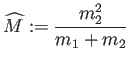
![]() ならば、
ならば、