3 クラドニ図形

クラドニ図形とは、 振動する板にまいた砂 (やそれに類する粉) が作る印象的なパターンのことです。

桂田研で取り扱うことになった発端は、 小学生向きの理科の図鑑 [71] の中の1頁だった (他に Waller [22], [23])。

図 3: Chladni

図 4: Chladni figures by himself

図 5: Waller の実験結果

図 6: 平野の差分法による数値計算結果

物理的には、いわゆる固有振動の節を見ていることになります。 それは数学的には、 振動を記述する偏微分方程式を Fourier の方法で解いた時に現れる 固有値問題

$$\Laplacian^2 u=\lambda u$$   in $\Omega$ $$,$$   $\rd\Omega$ における境界条件 (詳しいことは省略)

の固有関数 $\varphi$ が 0 となる点(節点)の集合 $\left\{(x,y)\mid \varphi(x,y)=0\right\}$ (普通は曲線になり、節線と呼ばれる) です。

$$\Laplacian^2=\left(\frac{\rd^2}{\rd x^2}+\frac{\rd^2}{\rd y^2}\ri... ...^2 =\frac{\rd^4}{\rd x^4}+2\frac{\rd^4}{\rd x^2\rd y^2}+\frac{\rd^4}{\rd y^4}$$

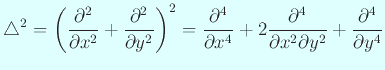
はいわゆるクロスタームを持つため、 考えている領域 $\Omega$ がたとえ正方形であっても、 厳密解を計算することは困難です。 そういう意味では、数値計算の格好の題材と言えるでしょう。

既に平野裕輝、小釜燈台君による研究があり (岡田・平野 [71], 平野 [25], 小釜 [79])、 正方形領域に対する差分法によるプログラム、 任意形状の領域に対する有限要素法によるプログラムがあります。

面白いのは対称性の高い領域について、 固有関数の対称性が崩れたりして固有値の重複度の問題が生じることです。

物理学者による興味深い「結果」-- 数学的には「予想」 -- (Waller [22]) があり、 それを数学的に証明できれば素晴らしいと思っています。

その種の証明を追及する以外にも、 正方形板以外の形でどうなるか調べることは研究する意義がありそうです (Waller [23] にはそのような実験結果も多数収録されています)。 (こちらは正方形の場合の「予想」を理解して、それに類するものが成り立つか、 数値実験的に調べるというアプローチがあります。)