- 71
-
鈴木敬信他(監修), 秋玲ニ(漫画):光・音・熱の魔術師, 集英社 (1963).
- 60
-
内藤智:円板領域,円の外部領域における代用電荷法の研究 --
通常スキームと不変スキームの比較,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2004-naitou.pdf (2005).
- 3
-
榊原航也:代用電荷法による正則関数の有理関数近似,
http://nalab.mind.meiji.ac.jp/~mk/labo/library/sakakibara/graduate_thesis.pdf (2012).
- 44
-
菊地文雄:有限要素法概説, サイエンス社 (1980), 新訂版 1999.
- 79
-
川野康一:非同次楕円型方程式,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/1995-kawano.pdf (1996).
- 79
-
高藤康孝:偏微分方程式の固有値問題,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/1997-takatou.pdf (1998).
- 71
-
鈴木康大:偏微分方程式の固有値問題の有限要素法による解法,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/1998-suzuki.pdf (1999).
- 79
-
川崎純也:熱伝導方程式の有限要素モデル,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/1995-kawasaki.pdf (1996).
- 79
-
石川邦臣:2次元熱方程式の有限要素法,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/1998-ishikawa.pdf (1999).
- 10
-
野沢崇:Stokes方程式の有限要素法,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/1997-nozawa.pdf (1998).
- 79
-
福嶋剛史:一般流束条件での定常 Navier-Stokes 方程式の数値解析,
明治大学大学院基礎理工学専攻数学系 修士論文,
http://nalab.mind.meiji.ac.jp/~mk/labo/members/pdf/Fukushima/fukushima-2005.pdf (2005).
- 79
-
工藤丈征:有限要素法による定常 Navier-Stokes 方程式の数値解析プログラム (Ver.1)
取り扱い説明書,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/kudou.pdf,
プログラム自身も
http://nalab.mind.meiji.ac.jp/~mk/labo/report/prog/kudou-prog-1.1.tar.gz に置いてある。一般公開の了承は取っていないので、パスワードつき。興味のある方はご相談下さい。LAPACK利用版もある。
(1995).
- 79
-
福澤誠人:定常Stokes方程式の有限要素解の事後誤差評価と事前誤差評価,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2004-fukuzawa.pdf (2005).
- 79
-
志賀浩二:数の大航海 -- 対数の誕生と広がり, 日本評論社 (1999).
- 79
-
カジョリ:復刻版 カジョリ 初等数学史, 共立出版 (1997), 小倉金之助 補訳.
- 16
-
Napier, J.: Mirifici Logarithmorum Canonis Descriptio (1614).
- 17
-
桂田祐史:桂田研卒業研究の歴史,
http://nalab.mind.meiji.ac.jp/~mk/labo/sotsugyou-report/ (1993~).
- 18
-
武田侑子:Napier の Descriptio の解読, MTS課題研究のレポート (2012/8/4).
- 19
-
Napier, J.: Mirifici Logarithmorum Canonis Constructio (1618).
- 20
-
Roegel, D.: Napier's ideal construction of the logarithms,
http://www.loria.fr/~roegel/publications.html (2011/11/12).
- 71
-
ニューワイドずかん百科 科学, 学習研究社 (2006).
- 22
-
Waller, M. D.: Vibrations of free square plates: part I. normal vibrating
modes, Proceedings of the Physical Society, Vol. Vol. 51, pp. 452-455
(1939).
- 23
-
Waller, M. D.: Chladni figures -- a study in symmetry, G. Bell and Sons
Ltd. (1961).
- 71
-
岡田卓, 平野裕輝:クラドニ図形, 2009年度桂田研卒業研究レポート (2010).
- 25
-
平野裕輝:クラドニ図形, 生明祭「これって数学なの!?」のポスター発表
(2010/11/20) (2010).
- 79
-
小釜燈台:クラドニ図形の数値解析, 明治大学理工学研究科 基礎理工学専攻 修士論文,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2013-kogama.pdf (2013).
- 71
-
島倉義和, 田邊雅人:球領域における熱方程式に対する差分法,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2006-shimakura-tanabe.pdf (2007).
- 28
-
Trott, M.: The Vibrating Ellipse-Shaped Drum, Mathematica Journal, Vol.
Volume 6, issue 4, pp. pp. 57-60 (1996).
- 44
-
山本てつろう哲朗:数値解析入門 [新訂版], サイエンス社 (2003), 1976
年初版発行の定番本の待望の改訂版.
- 79
-
金子裕司:S-W近似によって様々な領域の熱方程式を解くためのアルゴリズム,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2006-kaneko.pdf (2007).
- 71
-
久保田祥史:S-W近似によって様々な領域の熱方程式を解く,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2007-kubota.pdf (2008).
- 60
-
濱勇樹:S-W近似による楕円領域での波動方程式のシミュレーション,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2011-hama.pdf (2012).
- 33
-
Yamamoto, T., Fang, Q. and Chen, X.: Superconvergence and nonsuperconvergence
of the Shortley-Weller approximations for Dirichlet problems. International
Workshops on Numerical Methods and Verification of Solutions, and on
Numerical Function Analysis (Ehime/Shimane, 1999), Numer. Funct. Anal.
Optim., Vol. 22, no. 3-4, pp. 455-470 (2001).
- 34
-
Yamamoto, T.: A new insight of the Shortley-Weller approximation for
Dirichlet problems. Symbolic algebraic methods and verification methods
(Dagstuhl, 1999), pp. 245-253, Springer, Vienna (2001).
- 35
-
Yamamoto, T., Fang, Q. and Chen, X.: Superconvergence and nonsuperconvergence
of the Shortley-Weller approximations for Dirichlet problems,
数理解析研究所講究録, Vol. 1147, pp. 32-41 (2000).
- 36
-
Matsunaga, N. and Yamamoto, T.: Superconvergence of the Shortley-Weller
approximation for Dirichlet problems, J. Comput. Appl. Math., Vol. 116,
no. 2, pp. 263-273 (2000), 明治大学では Science Direct から入手可能。
- 37
-
Fang, Q., Shogenji, Y. and Yamamoto, T.: Error Analysis of Adaptive Finite
Difference Methods Using Stretching Functions for Polar Coordinate Form of
Poisson-Type Equation, Numer. Funct. Anal. Optim., Vol. 24, no. 1-2,
pp. 17-44 (2003).
- 38
-
Li, Z.-C., Hu, H.-Y., Fang, Q. and Yamamoto, T.: Superconvergence of solution
derivatives for the Shortley-Weller difference approximation of Poisson's
equation. II. Singularity problems, Numer. Funct. Anal. Optim., Vol.
24, no. 3-4, pp. 195-221 (2003).
- 39
-
Li, Z.-C., Yamamoto, T. and Fang, Q.: Superconvergence of solution derivatives
for the Shortley-Weller difference approximation of Poisson's equation. I.
Smoothness problems, J. Comput. Appl. Math., Vol. 151, no. 2, pp.
307-333 (2003), 明治大学では Science Direct から入手可能。
- 71
-
西條敏美:虹 -- その文化と科学, 恒星社厚生閣 (1999).
- 71
-
松山周五郎:音のFourier解析, 2003年度卒業研究レポート,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2003-matsuyama.pdf (2004).
- 71
-
難波 精一郎編:音の科学, 朝倉書店 (1989).
- 71
-
太田高正:ピアノ弦の性質と調律曲線, 数学セミナー, 2007年12月号, pp. 37-41
(2007).
- 44
-
城戸健一:ディジタルフーリエ解析(I) -- 基礎編 --, コロナ社 (2007).
- 45
-
城戸健一:ディジタルフーリエ解析(II) -- 上級編 --, コロナ社 (2007).
- 71
-
川口和也, 中井幹雄:打弦時に発生するインハーモニシティに関する研究,
日本機会学会 Dynamics and Design Conference 2001 CD-ROM論文集,
http://www.jsme.or.jp/monograph/dmc/2001/data/pdf/729.pdf (2001).
- 47
-
桂田祐史:音の取り扱いに関するメモ (C,Java,Mathematica),
http://nalab.mind.meiji.ac.jp/~mk/labo/text/memo-sound.pdf (2008~).
- 71
-
土橋光義:Sound and Temperament Lab
ピアノの音と音律:http://park11.wakwak.com/~md440/.
- 49
-
引地孝文, 小坂直敏:物理モデルによるピアノ音とギター音のモーフィングの検討,
音楽情報科学, Vol. 31-4, (1999).
- 71
-
橋本智樹, 梅谷征雄:ピアノ音の物理シミュレーション --
弦・駒・響板の連成解析をめざして --, 音楽情報科学, Vol. 34-1, (1999/2/17).
- 51
-
N. H.フレッチャー, T. D.ロッシング:楽器の物理学,
シュプリンガー・フェアラーク東京 (2002), 岸 憲史, 久保田 秀美, 吉川 茂 訳.
- 79
-
石川邦臣:半線形熱方程式に対する精度保証付き数値計算, 2000年度修士論文,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/ishikawa-master.pdf (2001).
- 79
-
鈴木康大:半線形楕円型偏微分方程式に対する精度保証付き数値計算,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/suzuki-master.pdf (2003).
- 79
-
佐藤晴郎:区間演算をサポートしたプログラミング言語の設計と処理系の実装,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/satou-master.pdf (2003).
- 60
-
礒野譲:連立一次方程式の解の精度保証付き数値計算,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/isono-master.pdf (2003).
- 62
-
牧野淳一郎:とんでる力学, 丸善 (2005).
- 79
-
石川雅基:ボールの軌跡,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2010-ishikawa.pdf (2011).
- 60
-
野地誠:流体中に置かれた回転円柱の運動,
http://nalab.mind.meiji.ac.jp/~mk/labo/2011/library2011/08nozi.pdf (2009).
- 59
-
野地誠:流体中に置かれた回転円柱の運動, 講演資料,
http://nalab.mind.meiji.ac.jp/~mk/labo/2011/library2011/08nozi_p.pdf (2009).
- 60
-
南大介:変化球の数理解析,
http://nalab.mind.ryukoku.ac.jp/~tsutomu/graduate/2009/09_minami.pdf (2010).
- 61
-
田端正久:流体問題の有限要素解析 -- 抗力・揚力係数を精度良く求める, 数理科学,
Vol. No.417, pp. 13-19 (1998),
http://nalab.mind.meiji.ac.jp/~mk/labo/members/pdf/Tabata/1998-tabata.pdf.
- 62
-
はった八田なつお夏夫:流れの計算, 森北出版 (1994/10).
- 63
-
山本哲朗:2点境界値問題の数理, コロナ社 (2006).
- 71
-
加藤敏夫:変分法, 岩波書店 (1960), 寺沢貫一「自然科学者のための数学概論 --
応用編 --」のC編.
- 79
-
清水康生:πの数値解析,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2003-shimizu.pdf (2004).
- 71
-
鎌田伊織, 吉本清夏:π ~計算法の変遷~,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2005-kamata-yoshimoto.pdf (2006).
- 79
-
椎名信治:Taylor展開による平方根計算と建部の円周率計算の解析,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2005-shiina.pdf (2006).
- 71
-
岡本久:非線形力学 第I部「流体の運動と力学系」, 岩波書店 (1995),
岩波講座応用数学の分冊.
- 69
-
稲垣亜希子, 栗田智昭, 田中賢史:渦糸の力学系,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/2002-inagaki-kurita-tanaka.pdf (2003).
- 79
-
中島大介:魚種交替の「3すくみ関係」,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2011-nakashima.pdf (2012).
- 71
-
長谷川成実:生物の増殖についての常微分方程式,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/2011-hasegawa.pdf (2012).
- 72
-
May, R. M. and Leonard, W. J.: Nonlinear Aspects of Competition Between Three
Species, SIAM Journal on Applied Mathematics, Vol. 29, pp. 243-253
(1975).
- 73
-
Schuster, P., Sigmund, K. and Wolff, W.: On
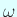 -Limits for Competition
Between Three Species, SIAM Journal on Applied Mathematics, Vol.
Vol. 37, No. 1, pp. 49-54 (1979).
-Limits for Competition
Between Three Species, SIAM Journal on Applied Mathematics, Vol.
Vol. 37, No. 1, pp. 49-54 (1979).
- 74
-
CHI, C.-W., HSU, S.-B., and WU, L.-I.: On the Asymmetric May-Leonard Model of
Three Competing Species, SIAM J. APPL. MATH., Vol. Vol. 58, No. 1, pp.
211-226 (1998).
- 79
-
渡邊隆之:戦闘における Lanchester の法則,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2010-watanabe-takayuki.pdf (2011).
- 76
-
Engel, J. H.: A Verification of Lanchester’s Laws, Journal of the
Operations Research Society of America, Vol. Vol.2, No.2, pp. 49-52 (1954).
- 79
-
皆川幸弘:ベルヌーイ数とその応用,
http://nalab.mind.meiji.ac.jp/~mk/labo/report/open/2005-minagawa.pdf (2006).
- 78
-
Driscoll, T. A. and Trefethen, L. N.: Schwarz-Christoffel Mapping,
Cambridge University Press (2002/8/15).
- 79
-
桂田祐史:微分方程式の解の爆発問題への入門,
http://nalab.mind.meiji.ac.jp/~mk/labo/2011/library2011/blowup/blowup.pdf (1996).
- 80
-
Nakagawa, T.: Blowing up of a Finite Difference Solution to
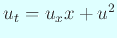 ,
Applied Mathematics & Optimization, Vol. Vol. 2, No. 4, (1976).
,
Applied Mathematics & Optimization, Vol. Vol. 2, No. 4, (1976).
- 81
-
Yun-Gang, C.: Asymptotic behaviours of blowing-up solutions for finite
difference analogu of
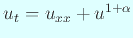 , J. Fac. Sci. Univ.
Tokyo, Sect. IA, Math., Vol. 33, pp. 541-574 (1986).
, J. Fac. Sci. Univ.
Tokyo, Sect. IA, Math., Vol. 33, pp. 541-574 (1986).
桂田 祐史
2017-04-29