正方形領域
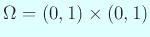 における
における
の固有関数は
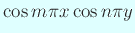
(
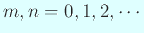
)
 に対して、
に対して、
とおく。
以下のことは容易に証明できる。
- (I)
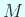 は完全直交系である。
は完全直交系である。
- (II)
-
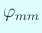 の節線
の節線
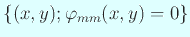 は完全な対称性を持つ (二面体群
は完全な対称性を持つ (二面体群 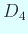 の任意の要素に関して
不変)
の任意の要素に関して
不変)
- (III)
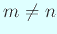 ,
, 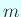 と
と 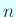 は共に偶数か共に奇数とするとき、
は共に偶数か共に奇数とするとき、
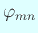 の節線は完全な対称性を持つ。
それにもかかわらず
の節線は完全な対称性を持つ。
それにもかかわらず
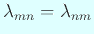 .
.
- (IV)
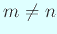 ,
, 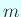 と
と 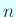 は一方が偶数で他方が奇数とするとき、
は一方が偶数で他方が奇数とするとき、
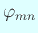 の節線は完全な対称性を持たない。
の節線は完全な対称性を持たない。
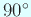 の回転について不変でなく、
の回転について不変でなく、
 の節線になる。
の節線になる。
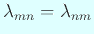 .
.
一方、板の固有値問題については、固有関数の族
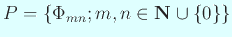 で、以下の性質を持つものが存在する、
と Waller [22] には書いてあるように読める。
で、以下の性質を持つものが存在する、
と Waller [22] には書いてあるように読める。
- (i)
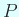 は完全直交系である。
は完全直交系である。
- (ii)
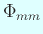 の節線
の節線
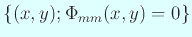 は完全な対称性を持つ
(二面体群
は完全な対称性を持つ
(二面体群 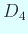 の任意の要素に関して不変)
の任意の要素に関して不変)
- (iii)
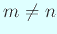 ,
, 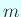 と
と 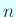 は共に偶数か共に奇数とするとき、
は共に偶数か共に奇数とするとき、
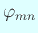 の節線は完全な対称性を持つ。
の節線は完全な対称性を持つ。
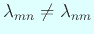 .
.
- (iv)
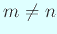 ,
, 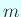 と
と 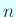 は一方が偶数で他方が奇数とするとき、
は一方が偶数で他方が奇数とするとき、
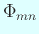 の節線は完全な対称性を持たない。
の節線は完全な対称性を持たない。
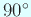 の回転について不変でなく、
の回転について不変でなく、
 の節線になる。ゆえに対応する固有値は重根である。
の節線になる。ゆえに対応する固有値は重根である。
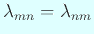 .
.
このことを数学的に証明し、 (III) と(iii) の相違の原因を理解したい。
桂田 祐史
2017-04-29
![]() における
における
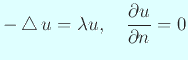
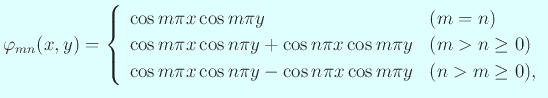
![]() で、以下の性質を持つものが存在する、
と Waller [22] には書いてあるように読める。
で、以下の性質を持つものが存在する、
と Waller [22] には書いてあるように読める。