- ... を1次元的に並べて番号をつけた1
-
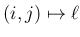 の逆変換は、
の逆変換は、
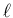 を
を 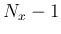 で割った余りと商を
で割った余りと商を 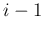 ,
, 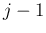 とすれば良い。
とすれば良い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... の原理2
- なんでも、
Dirihlet 先生の講義に出て来たのだとか。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... の積分公式3
- Greenの積分公式とは、
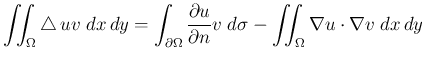 と言うもの。
これは発散定理
と言うもの。
これは発散定理
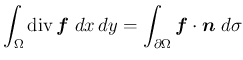 に、
に、
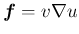 を代入すれば得られる。
を代入すれば得られる。
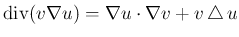 ,
,
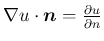 であることに注意する。
であることに注意する。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...次に変分問題4
- 変分法を知らない人のために説明: 汎函数(関数を変数
とする関数のこと) の最小値問題を変分問題と呼ぶ。ここでは、
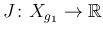 が汎函数で、
が汎函数で、
 は
は 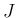 の最小値を与える点となっている。
の最小値を与える点となっている。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...写像関数と呼ぶ
5
- 関数論において等角写像とは、いたるところ
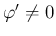 を
満たす正則関数のことを指す。一対一の等角写像
を
満たす正則関数のことを指す。一対一の等角写像
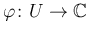 があるとき、終域を
があるとき、終域を
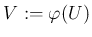 で置き換えた、
で置き換えた、
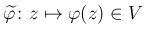 は双正則である
(
は双正則である
(
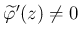 が簡単に導かれる)。
しばしば、等角写像という言葉を、双正則な関数の意味に使うことがある。d
が簡単に導かれる)。
しばしば、等角写像という言葉を、双正則な関数の意味に使うことがある。d
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... と呼ぶ6
- その理由は、
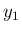 ,
, 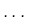 ,
, 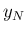 それぞれに電荷量
それぞれに電荷量 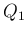 ,
,  ,
, 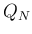 の電荷を置いたとき、それら電荷の作る電場のポテンシャルが
の電荷を置いたとき、それら電荷の作る電場のポテンシャルが  であ
る、という事実に基づく。
であ
る、という事実に基づく。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
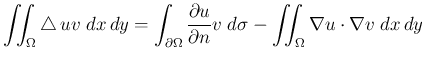 と言うもの。
これは発散定理
と言うもの。
これは発散定理
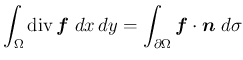 に、
に、