Next: 5.10.4 魚種交替 Up: 5.10 Lotka-Volterra 方程式に続いて Previous: 5.10.2 2種競争系
May-Leonard は、[11] (1975年) の中で3種の生物が競争するモデルを提唱し、 解が興味深い挙動を持つことを示した。
![$\displaystyle \left\{ \begin{array}{ll} \dfrac{\D N_1}{\D t}=N_1(1-N_1-\alpha N...
...[2ex] \dfrac{\D N_3}{\D t}=N_3(1-\alpha N_1-\beta N_2- N_3) \end{array} \right.$](img343.png) |
(5.17) |
![]() ,
, ![]() は正の定数である。
は正の定数である。
これを
![]() で考察する。
で考察する。
この力学系の平衡点の安定性、
![]() のときの解の漸近挙動について詳しいことが分かっている。
シミュレーションをすると楽しめる。
のときの解の漸近挙動について詳しいことが分かっている。
シミュレーションをすると楽しめる。
平衡点は8つあるが、何種が生き残っているかで分類すると次のようになる。
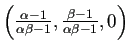 ,
,
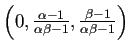 ,
,
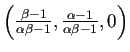 .
.
これらが ![]() に属するには、
に属するには、![]() ,
, ![]() が
が
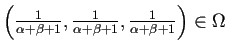 .
.
まとめ直すと
(c), (e) の場合に、初期値が平衡点でなければ、 3つの1種平衡点(の近く)を巡回する解が存在する。 一見周期解のようにも見えるが、 だんだん1種平衡点の近くに逗留する時間が長くなる。
上の不等式は等号なしの場合であるが、
等号つきの場合にも重要なものがある。
特に
![]() のとき、
のとき、
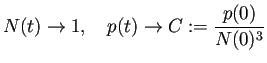
May-Leonard のモデルを修正した研究として Jaramillo-Mrad-Stepien [12] がある。
桂田 祐史