Next: 6 SIRモデル Up: 5.10 Lotka-Volterra 方程式に続いて Previous: 5.10.3 3種競争系
魚種交替と呼ばれる現象がある。
マイワシ、カタクチイワシ、マサバの3種類のうきうお浮魚類 (海の表層に住んでいて、プランクトン食) の日本近海における個体数は、数十年単位で変動し、 沖合ではどれか一種だけが分布を広げている。 この優占する魚種が交替する現象を魚種交替 (species replacement) と呼ぶ (河井 [13], [14], 川崎 [15])。
魚種交替は、 3すくみの競争関係にある力学系モデル
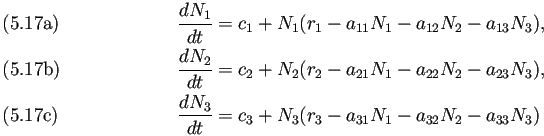 |
![]() は内的自然増加率、
は内的自然増加率、
![]() は種
は種 ![]() が種
が種 ![]() に与える負の影響の強さを表す。
それぞれの魚種には、相手に侵されない(競争せずにすむ)「聖域」があり、
微小な正の定数である
に与える負の影響の強さを表す。
それぞれの魚種には、相手に侵されない(競争せずにすむ)「聖域」があり、
微小な正の定数である ![]() は“聖域からの補給” を表す。
聖域がないと、低水準期の資源量が減り過ぎて、種の存続が危うくなる。
浮魚3種は沖合の回遊域をめぐっては競争しているが、
沿岸域はそれぞれの聖域として残っている。
は“聖域からの補給” を表す。
聖域がないと、低水準期の資源量が減り過ぎて、種の存続が危うくなる。
浮魚3種は沖合の回遊域をめぐっては競争しているが、
沿岸域はそれぞれの聖域として残っている。
May-Leonard のモデルでは、1種平衡点を巡回する解が、
時間の経過とともに平衡点に近づくことで、その近傍に長く逗留するようになったが、
正の ![]() を入れることにより、1種平衡点に近づきすぎなくなる効果が生じ、
周期的な解が存在しやすくなる。
を入れることにより、1種平衡点に近づきすぎなくなる効果が生じ、
周期的な解が存在しやすくなる。
このモデルは、May-Leonard のモデルとは色々違っているけれど、 重要な違いは聖域からの供給効果を導入しているところと考えられる。 そこで、 May-Leonard のモデルに聖域からの供給効果だけを加えたモデル
![$\displaystyle \left\{ \begin{array}{ll} \dfrac{\D N_1}{\D t}=c+N_1(1-N_1-\alpha...
...ex] \dfrac{\D N_3}{\D t}=c+N_3(1-\alpha N_1-\beta N_2- N_3) \end{array} \right.$](img378.png) |
(5.19) |