4.5 Python, Julia で数値計算

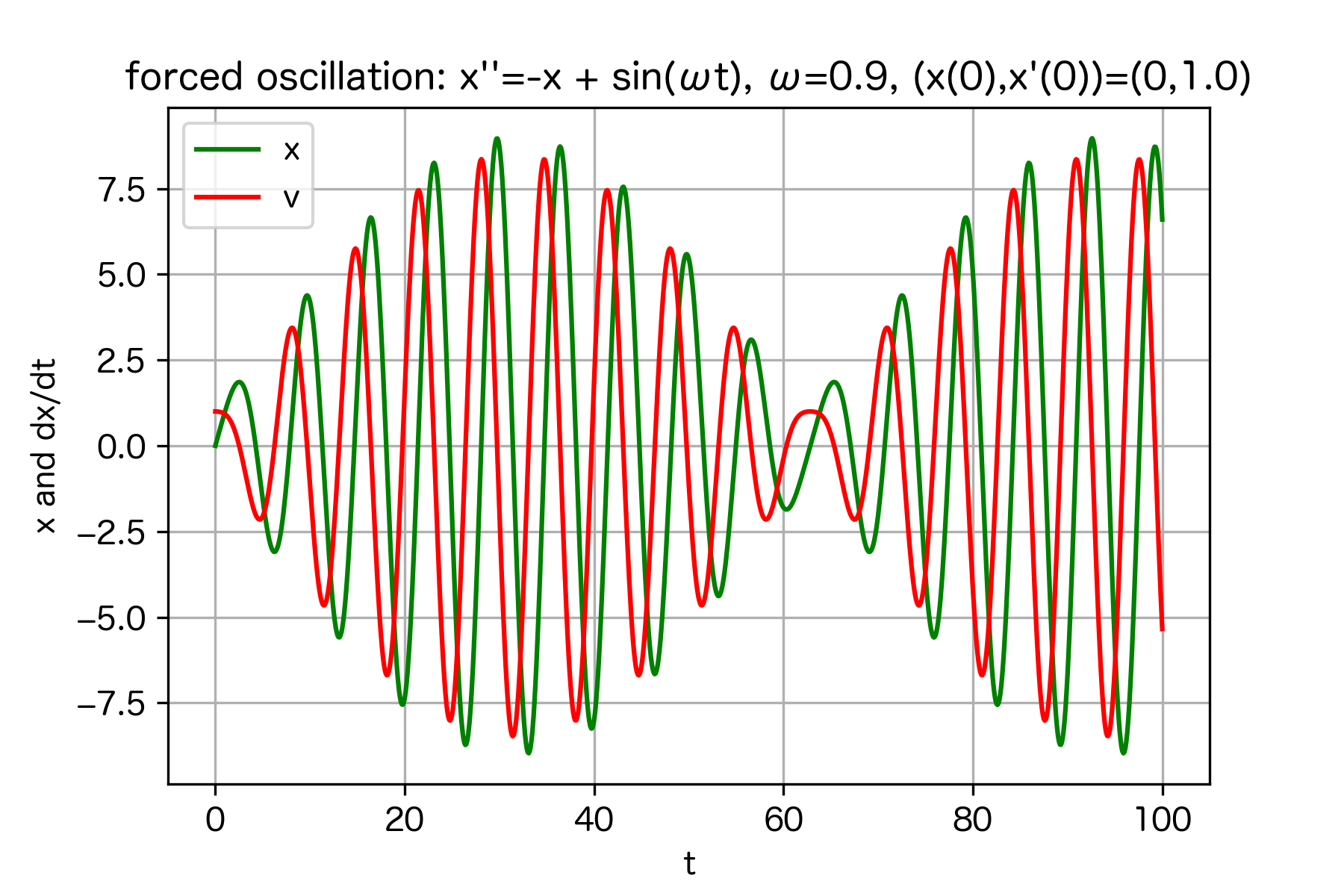
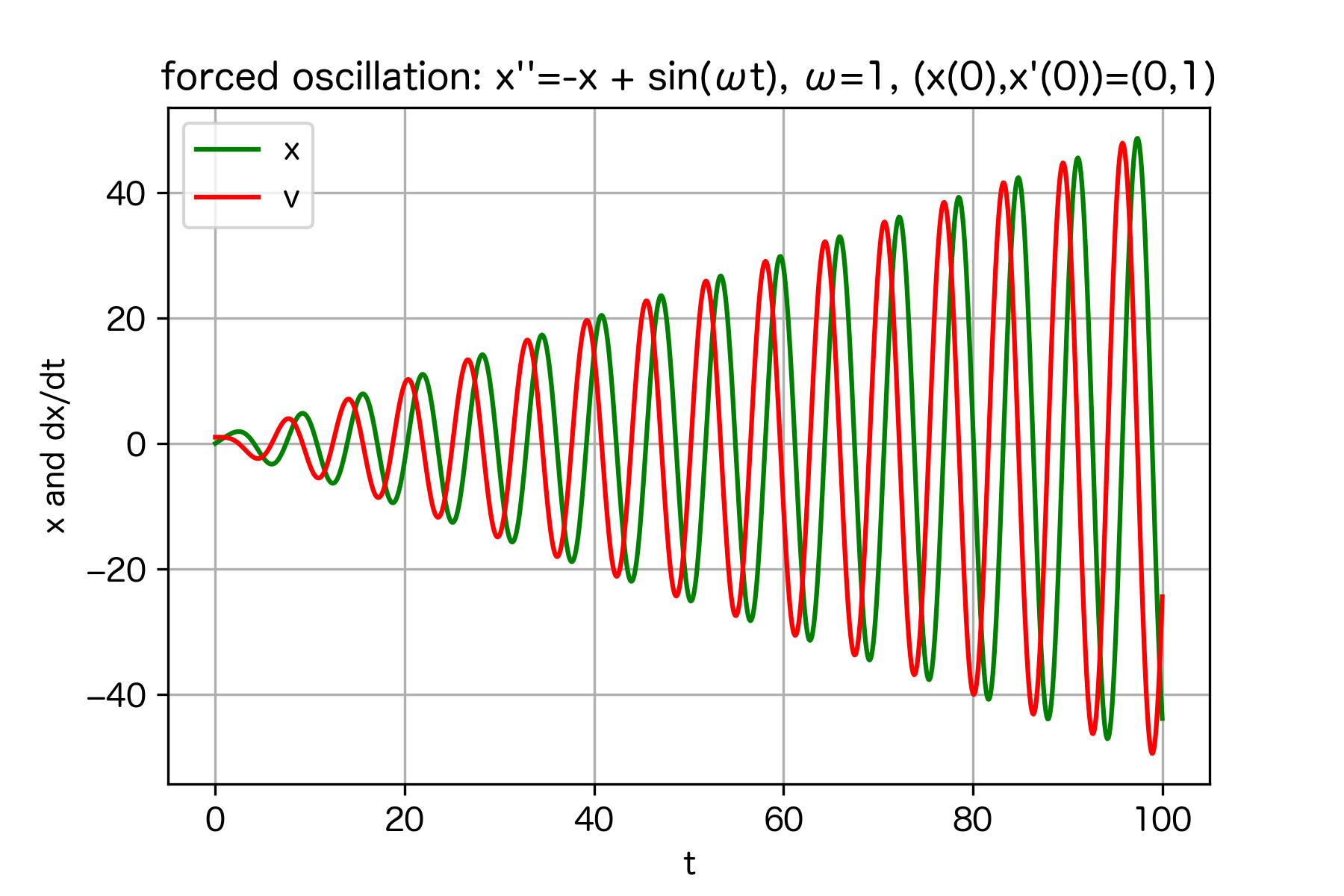
常微分方程式の初期値問題は、 素朴な Runge-Kutta 法のプログラムで十分に解ける場合が多いので、 そういう取り組みを勧めるテキストが少なくないが (例えばネットで読める桂田 [4])、 現在普及している Python や Julia には、 常微分方程式の初期値問題の高品質なソルバーが搭載されていて、 可視化をするにも便利なので、それらを利用するのを強く勧めたい (私は宗旨替えをしました)。 ここでは Python, Julia のサンプル・コードを示す (付録B 参照)。

課題 4.5.1   減衰振動の方程式

$$x''(t)+k x'(t)+\omega^2 x(t)=0,\quad x(0)=x_0,\quad x'(0)=v_0$$

のシミュレーションをするプログラムを作成し、 実際にシミュレーションをするプログラムせよ。

課題 4.5.2   強制振動の方程式

$$x''(t)+\omega^2 x(t)=F\sin\omega' t,\quad x(0)=1,\quad x'(0)=0$$

のシミュレーションをするプログラムを作成し、 $\omega\ne\pm\omega'$ のとき、 $\omega=\omega'$ のときをシミュレーションしてみよ。 (厳密解の求め方は https://m-katsurada.sakura.ne.jp/lecture/kiso4/kiso4ode.pdf#page=126(の問題5とその3ページ後の解答) に載っている。)

図 4: 強制振動 ( $\omega '\ne \pm 1$)

図 5: 強制振動 ($\omega '=1$)