Next: F..8 線形非同次方程式の解空間の構造 Up: F. 線形微分方程式の常識 Previous: F..6 線形同次方程式の解空間の次元
![]() ,
,
![]() ,
,
![]() とするとき、常微分方程式
とするとき、常微分方程式
![]() の相異なる根を
の相異なる根を ![]() ,
, ![]() ,
, ![]() とすると
とすると
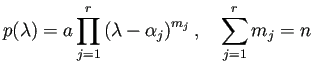
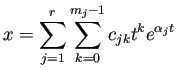 (
(
![\begin{jlemma}
\begin{enumerate}[(1)]
\item
$(D-\alpha)\left(e^{\alpha t}\varph...
...lpha t}\varphi(t)\right)=e^{\alpha t}D^m\varphi(t)$.
\end{enumerate}\end{jlemma}](img951.png)
|
((1) を
![]() と書くと、
と書くと、
![]() となり (2) が分かりやすいかも、とか色々考えるけれど、
決定版が見つかっていない感がある。)
となり (2) が分かりやすいかも、とか色々考えるけれど、
決定版が見つかっていない感がある。)

|
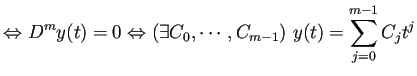 |
||
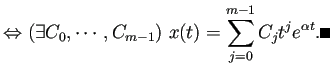 |
![]() なる
なる![]() に対して、
に対して、
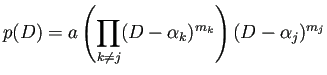
1次独立性の証明は難しくはないが、一般的に記述しようとすると、 (添字が増えて) 式が複雑になり、議論が分かりにくく感じる人が多くなると思われる。 以下では、特別な場合に証明する (それが理解出来れば一般の場合に成り立つことが理解できると思われる)。
まず補題を準備する。
![\begin{jlemma}
\begin{enumerate}[(1)]
\item
$f(\lambda)\in\mathbb{C}[\lambda]$, ...
...t{($k>\ell$)}.
\end{array} \right.
\end{displaymath}\end{enumerate}\end{jlemma}](img978.png)
|
![$\displaystyle (D-\alpha)^\ell\left[t^ke^{\alpha t}\right]
=e^{\alpha t}e^{-\al...
...ha t}t^k
=e^{\alpha t}D^\ell t^k=e^{\alpha t}\frac{k!}{\ell!}t^{k-\ell}. \qed
$](img980.png)
1次独立性の証明のあらすじ
![]() ,
, ![]() ,
, ![]() が相異なるとき、
が相異なるとき、
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() が1次独立であること、
すなわち
が1次独立であること、
すなわち
![]() を示す (
を示す (![]() や
や ![]() の証明も同様である)。
の証明も同様である)。
桂田 祐史