- ...
を考える1
- (1) は
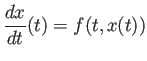 と書く方が誤解がないかもしれないが、
と書く方が誤解がないかもしれないが、
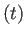 は省略されることが多い。
は省略されることが多い。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... を求めることを目標とする2
- つまり、変数
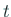 の離散的な値に対する解の値のみを求める、という意味で「離散変数法」なわ
け。このように目標を低く設定することによって、無限次元の問題が有限次元
の問題に簡略化されていると言える。
の離散的な値に対する解の値のみを求める、という意味で「離散変数法」なわ
け。このように目標を低く設定することによって、無限次元の問題が有限次元
の問題に簡略化されていると言える。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 法である3
- 単に Euler 法と呼ばれることも多いが、後退Euler法
というものがあるので、それと区別するために前進Euler法と呼ばれる。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 法という4
- Runge-Kutta法にはたくさんの親戚がいるので、
ここで紹介したものを、
「古典的Runge-Kutta法」、「4次のRunge-Kutta法」と呼ぶこともある。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...微分方程式は、他の諸科学への応用のみならず5
- 微分方程式は、
物理学の問題を扱うために発明されましたが、
現在では自然科学以外でも応用されています。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
数学それ自体にとっても非常に重要です6
- 常微分方程式の簡単なものは、
高等学校でも学びましたし (これはいつの学習指導要領かによる)、
1 年次にも微分方程式という授業がありました。
数学科の 3 年次にもより詳しいことを学ぶための講義があります。
常微分方程式に対する参考書は色々ありますが、例えば、
3 年生向けの講義の教科書になっている、
笠原晧司著「微分方程式の基礎」朝倉書店、をあげておきます。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
これはコンピューターによる数値シミュレーション7
- simulation(模擬実験)を
「シュミレーション」と読み間違えないでください。
「シミュレーション」ですからね。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...常微分方程式としては正規形8
- 方程式が最高階の導関数について解
かれている、ということですが、よく分からなくても差し支えありません。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...差分方程式9
- 漸化式のようなものだと思って構いません。
差分とは、高等学校の数列で言う階差のことです。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
が証明できます10
- 現在の数学科のカリキュラムでは 3 年次に開講さ
れている常微分方程式の講義で学びます。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
はありません11
- 配列はメモリーを消費しますし、(特に Fortran の場
合、配列の大きさは実行時に変更できないので)プログラムを書く際に、どれ
くらいの大きさの配列を用意したらいいのかという問題に悩まなくてはなりま
せん。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...このプログラムをコンパイルして12
- コンパイルすると、
“reidai5-1.c:34: warning: unused parameter `t'”
という警告メッセージが出ますが、大丈夫です
(言っていることは確かにもっともですが)。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
別な場合13
- 例えば微分方程式の右辺に現れる関数
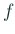 が、解析的な
式で定義された滑らかなものではなく、実験により計測されたデータにより定
義されている場合等は、高精度の公式を用いるよりも、Euler 法の方が良いこ
とがあります。
が、解析的な
式で定義された滑らかなものではなく、実験により計測されたデータにより定
義されている場合等は、高精度の公式を用いるよりも、Euler 法の方が良いこ
とがあります。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (かもしれません)14
- これは Java で書かれたアプレットです。
ソースは http://nalab.mind.meiji.ac.jp/~mk/labo/java/prog/ODE1.java
にあります。 -- (2021/4/1追記)
現在では、セキュリティ上の理由で、
このような Java アプレットの利用は認められなくなりました。
残念ながら実行できなくなっています。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
とおくと15
- 今回は
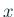 がベクトルであることを強調するために矢印
がベクトルであることを強調するために矢印
 をつけて
をつけて 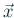 と書きます。
と書きます。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... space)16
- “phase
space” は数学以外の本では「位相空間」と訳されることが多いですが、数学
では「相空間」という訳語を用います。
「位相空間」という言葉は数学では “topological space” の訳語に使われるからでしょう。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...dynamical17
- “mechanics” の「力学」ではありません。
“dynamical” は「動的」という意味で、“statical” の反対語です。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... での流れの速度18
-
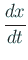 は速度を意味することは分かりま
すね?
は速度を意味することは分かりま
すね?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Pol19
- ファンデルポール、と読みます。
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
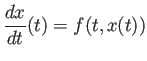 と書く方が誤解がないかもしれないが、
と書く方が誤解がないかもしれないが、