5.1.3.1 例題8-2

van der Pol¹⁹ の方程式 $x''+\mu(x^2-1)x'+x=0$ ($\mu$ は正定数)を一階に直して出来る力学系

$$\frac{d}{dt}{x \choose y}={y\choose -x + \mu(1 - x^2)y} \leqno{(3)}$$

の流れの様子を $-5\le x,y\le 5$ の範囲で描きなさい。

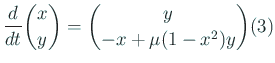
上の例題と同様にreidai8b-glsc.cというプログラムと rei8b.data というサンプル・データを用意してあります。 それを使って描いた図が図9です。

試してみよう

curl -O http://nalab.mind.meiji.ac.jp/~mk/program/ode_prog/reidai8b-glsc.c
cglsc reidai8b-glsc.c
curl -O http://nalab.mind.meiji.ac.jp/~mk/program/ode_prog/rei8b.data
cat rei8b.data | ./reidai8b-glsc

図 9: van der Pol の方程式の相図

原点を回っている一つの閉軌道が目につきますが、特徴的なのは、 その付近の軌道が、閉軌道にまつわりついて行っていることです。 描画中の図を眺めていると分かりますが、 どこからスタートしても速やかに閉軌道に近付いていきます。 この種の閉軌道(サイクル)のことをリミット・サイクル (極限閉軌道、limit cycle) と呼びます。

時間が経つと、はるか彼方に飛んでいってしまうような現象は別にして、 時間によって変化する現象のうちの多くのものは長い時間が経つと、 ある停止状態に落ち着くか（沈点）、周期運動（極限閉軌道）に落ち着きます。 2次元の常微分方程式という簡単なモデルで、 そういう現象を見ることが出来たわけです。